Chapter 10 분류규칙의 성능 평가
도출된 분류규칙에 대한 평가는 범주를 아는 학습표본이 있으므로 비교적 용이하게 이루어진다. 분류정확도 또는 분류오류율이 기본이 되나, 특히 범주가 2개인 경우에는 다양한 성능평가척도가 개발되어 사용되고 있다.
10.1 필요 R 패키지 설치
본 장에서 필요한 R 패키지들은 아래와 같다.
| package | version |
|---|---|
| tidyverse | 1.3.1 |
| caret | 6.0-88 |
10.2 분류오류율
범주를 아는 데이터 \(\{(\mathbf{x}_i, y_i)\}_{i = 1, \cdots, N}\)를 학습표본이라 한다.
- \(\mathbf{x}_i\): \(p\)개의 독립변수로 이루어진 \(i\)번째 객체의 변수벡터 (\(\mathbf{x}_i = [x_{i1} \, x_{i2} \, \cdots \, x_{ip}]^\top\))
- \(J\): 총 범주 수
- \(y_i\): \(i\)번째 객체의 범주 변수; \(y_i \in \{1, 2, \cdots, J\}\)
분류규칙 \(d(\mathbf{x})\)의 성능은 주로 분류오류율(misclassification rate)을 사용하는데, 분류규칙이 추정한 범주와 실제범주가 일치하지 않는 비율을 나타낸다.
\[\begin{equation} R(d) = \frac{1}{N} \sum_{i = 1}^{N} I(d(\mathbf{x}_i) \neq y_i) \tag{10.1} \end{equation}\]
여기서 함수 지시함수 \(I(x)\)는 \(x\)가 참(true)일 때 1, 거짓(false)일 때 0의 값을 갖는다.
식 (10.1)은 학습표본에 대한 오분류율로, 이를 최소화하려할 경우 분류규칙이 해당 학습데이터에만 과적용(overfitting)되는 문제가 발생할 수 있다. 즉, 새로운 데이터에 적용할 때도 오분류율이 최소화될 것이라는 보장이 없다.
이 때문에, 통상 관측수가 상당수 있는 데이터에 대해서는 전체 데이터를 두 부분으로 나누어, 분류규칙을 만드는 데 한 부분을 사용하고, 분류오류율을 산출하는 데 다른 한 부분을 사용하는 방안이 일반적이다. 아래와 같이 범주가 알려져있지만 분류규칙 \(d(\mathbf{x})\)를 학습하는 데 사용하지 않은 \(L\)개의 테스트 표본 \(\{(\mathbf{x}_i, y_i)\}_{i = N + 1, \cdots, N + L}\)이 있다고 하자. 이 때 테스트 표본에 대한 분류오류율을 아래와 같이 계산한다.
\[\begin{equation} R^{ts}(d) = \frac{1}{L} \sum_{i = N + 1}^{N + L} I(d(\mathbf{x}_i) \neq y_i) \tag{10.2} \end{equation}\]
테스트 표본으로 분리하기에 충분하지 않은 데이터의 경우에는 cross validation 기법을 사용한다.
10.3 정확도, 민감도 및 특이도
의학 분야에서 어떤 질병에 대한 진단방법을 평가할 때 오류율 이와에 정확도, 민감도 및 특이도를 분석하는 경우가 종종 있다. 실제범주가 질병이 있는 경우(1 또는 +로 표기)와 질병이 없는 경우(0 또는 -로 표기)의 두 가지로 분류된다고 하고, 진단 방법이 양성(1 또는 +) 또는 음성(0 또는 -)으로 판정할 때, 아래와 같이 네 가지 경우가 발생한다. 이와 같은 표를 정오분류표(confusion matrix)라 한다.
cm <- matrix(c('a', 'b', 'c', 'd'), nrow = 2, byrow = TRUE)
attr(cm, "dimnames") <- list(Prediction = c("1", "0"), Reference = c("1", "0"))
class(cm) <- "table"
print(cm)## Reference
## Prediction 1 0
## 1 a b
## 0 c d위 표의 문자들은 다음과 같이 정의된다.
- \(a\): number of true positive prediction
- \(b\): number of false positive prediction
- \(c\): number of false negative prediction
- \(d\): number of true negative prediction
여기서 “positive” 또는 “negative”는 “양성” 또는 “음성”으로 추정됨을 나타내고, “true” 또는 “false”는 추정의 사실 또는 거짓을 나타낸다. 이 때 분류오류율은 다음과 같이 산출된다.
\[\begin{equation} \text{misclassifiction rate} = \frac{b + c}{a + b + c + d} \tag{10.3} \end{equation}\]
정확도(accuracy)는 오류율의 반대 개념으로, 실제 범주를 제대로 추정한 전체 비율을 나타내며 아래와 같이 산출된다.
\[\begin{equation} \text{accuracy} = \frac{a + d}{a + b + c + d} = 1 - \text{misclassifiction rate} \tag{10.4} \end{equation}\]
한편, 민감도(sensitivity)는 실제 질병이 있는 경우를 양성으로 판정하는 비율을 나타내는 것으로, 다음과 같이 산출된다.
\[\begin{equation} \text{sensitivity} = \frac{a}{a + c} \tag{10.5} \end{equation}\]
그리고 특이도(specificity)란 실제 질병이 없는 경우를 음성으로 판정하는 비율을 나타내는 것으로 다음과 같다.
\[\begin{equation} \text{specificity} = \frac{d}{b + d} \tag{10.6} \end{equation}\]
정확도를 민감도 및 특이도로 표현하면 다음과 같다.
\[\begin{equation*} \text{accuracy} = \frac{a + c}{a + b + c + d}\text{sensitivity} + \frac{b + d}{a + b + c + d}\text{specificity} \end{equation*}\]
민감도 및 특이도를 별도로 산출하여 분석하는 이유 중 하나는, 동일한 정확도를 갖는다 하더라도 민감도와 특이도는 다를 수 있기 때문이다. 경우에 따라서는 높은 민감도를 원하거나 높은 특이도를 원할 수 있다.
10.3.1 R 패키지 내 정오분류표
100개의 객체에 대한 실제범주와 추정범주가 아래와 같이 주어진다고 하자.
\[\begin{eqnarray*} y_i &=& \begin{cases} 1 & i = 1, \cdots, 20\\ 0 & i = 21, \cdots, 100 \end{cases},\\ \hat{y}_i &=& \begin{cases} 1 & i = 1, \cdots, 15, 91, \cdots, 100\\ 0 & i = 16, \cdots, 90 \end{cases} \end{eqnarray*}\]
y <- factor(c(rep(1, 20), rep(0, 80)), levels = c(1, 0))
y_hat <-factor(c(rep(1, 15), rep(0, 75), rep(1, 10)), levels = c(1, 0))해당 추정결과에 대한 정오분류표 및 각종 평가지표를 얻기 위해 caret 패키지의 confusionMatrix 함수를 이용한다.
cm <- caret::confusionMatrix(data = y_hat, reference = y)우선 정오분류표는 결과 객체의 table component에 저장된다.
cm$table## Reference
## Prediction 1 0
## 1 15 10
## 0 5 70정확도를 비롯한 각종 전반적인 지표는 overall이라는 component에 벡터 형태로 저장된다.
cm$overall## Accuracy Kappa AccuracyLower
## 0.8500000 0.5714286 0.7646925
## AccuracyUpper AccuracyNull AccuracyPValue
## 0.9135456 0.8000000 0.1285055
## McnemarPValue
## 0.3016996또한, 민감도, 특이도를 비롯한 몇 가지 분류성능 지표들은 byClass라는 component에 역시 벡터 형태로 저장된다.
cm$byClass## Sensitivity Specificity
## 0.7500000 0.8750000
## Pos Pred Value Neg Pred Value
## 0.6000000 0.9333333
## Precision Recall
## 0.6000000 0.7500000
## F1 Prevalence
## 0.6666667 0.2000000
## Detection Rate Detection Prevalence
## 0.1500000 0.2500000
## Balanced Accuracy
## 0.812500010.4 ROC 곡선
일반적으로 민감도와 특이도를 동시에 증가시키는 것은 불가능하다. 다시 말하면, 민감도를 높이면 특이도가 감소하고, 또한 반대가 성립하게 된다.
예를 들어 다음과 같이 10개의 객체로 이루어진 학습표본이 있다고 하자.
train_df <- tribble(
~x, ~y,
24, 0,
35, 0,
37, 1,
42, 0,
49, 1,
54, 1,
56, 0,
68, 1,
72, 1,
73, 1
) %>%
mutate(y = factor(y, levels = c(1, 0)))분류기준이 만약 \(x < 40\)이면 범주 0, \(x \geq 40\)이면 범주 1로 추정할 때, 정오분류표는 다음과 같다.
cm40 <- caret::confusionMatrix(
factor(as.integer(train_df$x >= 40), levels = c(1, 0)),
train_df$y
)
cm40$table## Reference
## Prediction 1 0
## 1 5 2
## 0 1 2이 때 구해지는 민감도 및 특이도는 아래와 같다.
cm40$byClass[c("Sensitivity", "Specificity")]## Sensitivity Specificity
## 0.8333333 0.5000000한편, 분류기준이 만약 \(x < 50\)이면 범주 0, \(x \geq 50\)이면 범주 1로 추정할 때, 정오분류표는 다음과 같다.
cm50 <- caret::confusionMatrix(
factor(as.integer(train_df$x >= 50), levels = c(1, 0)),
train_df$y
)
cm50$table## Reference
## Prediction 1 0
## 1 4 1
## 0 2 3또한, 이 때 구해지는 민감도 및 특이도는 아래와 같다.
cm50$byClass[c("Sensitivity", "Specificity")]## Sensitivity Specificity
## 0.6666667 0.7500000위 \(x\)값 40을 기준으로 분류를 하는 경우와 비교하여 민감도는 감소하고 특이도는 증가함을 관찰할 수 있다.
분류를 위한 \(x\) 기준값(threshold)을 증가시켜가면서 민감도와 특이도가 어떻게 변하는 지 살펴보도록 하자.
univariate_binary_rule <- function(x, y, th) {
cm <- caret::confusionMatrix(
factor(as.integer(x >= th), levels = c(1, 0)),
y
)
tibble(threshold = th,
sensitivity = cm$byClass["Sensitivity"],
specificity = cm$byClass["Specificity"])
}
th <- c(sort(train_df$x), Inf)
roc_df <- map_dfr(th, univariate_binary_rule, x = train_df$x, y = train_df$y)
knitr::kable(
roc_df, booktabs = TRUE,
align = c('r', 'r', 'r', 'r'),
col.names = c('분류기준값($x$)', '민감도(sensitivity)', '특이도(specificity)'),
caption = '분류기준별 민감도 및 특이도'
)| 분류기준값(\(x\)) | 민감도(sensitivity) | 특이도(specificity) |
|---|---|---|
| 24 | 1.0000000 | 0.00 |
| 35 | 1.0000000 | 0.25 |
| 37 | 1.0000000 | 0.50 |
| 42 | 0.8333333 | 0.50 |
| 49 | 0.8333333 | 0.75 |
| 54 | 0.6666667 | 0.75 |
| 56 | 0.5000000 | 0.75 |
| 68 | 0.5000000 | 1.00 |
| 72 | 0.3333333 | 1.00 |
| 73 | 0.1666667 | 1.00 |
| Inf | 0.0000000 | 1.00 |
민감도와 특이도를 동시에 그래프로 나타낸 것 중 ROC(receiver operating characteristic) 곡선이 널리 사용되는데, 이는 분류기의 경계치를 조정하여 가면서 (1 - 특이도)(또는 false positive rate)을 \(x\)축에, 민감도를 \(y\)축에 도식화한 것이다.
위 Table 10.1를 바탕으로 ROC 곡선을 작성해보자.
roc_df %>%
ggplot(aes(x = 1 - specificity, y = sensitivity)) +
geom_path()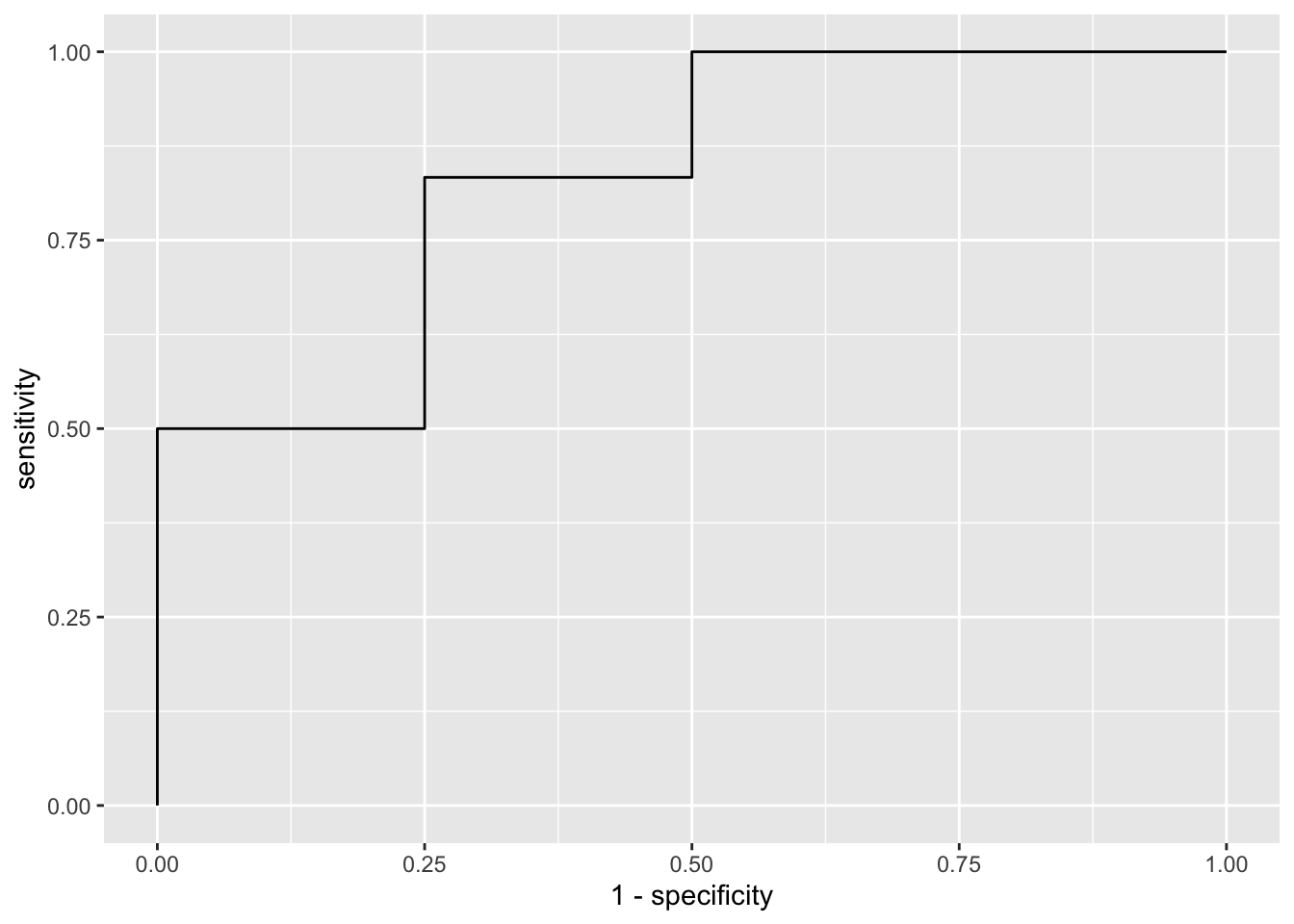
Figure 10.1: ROC 곡선
10.5 이익도표
이익도표는 마케팅을 위하여 수익을 창출하는 목표고객(target)을 추출할 목적으로 사용되는데, 단순히 분류를 위한 여러 모형을 비교하기 위한 목적으로도 종종 사용되고 있다. 목표 마케팅의 목적에서는, 특정 범주의 고객을 목표고객으로 할 때, 이러한 목표고객의 비율이 상대적으로 높은 서브그룹을 찾고자 하는 것이다. 이를 위해, 우선 전체 데이터를 특정 범주의 사후확률의 순서로 정렬한 후, \(K\)개(주로 \(K = 10\)을 사용)의 집단으로 구분하고, 각 집단별로 다음과 같은 통계량을 산출한다.
\(k\)번째 집단 내에서 범주 \(j\)에 속한 객체의 수를 \(n_{kj}\)라 할 때, 다음과 같은 범주 \(j\)에 대한 \(k\)번째 집단의 통계량들을 산출할 수 있다. (본 장에서 \(K\)개의 집단은 동일한 크기라 가정하자. 즉, 모든 집단 \(k\)에 대해 \(\sum_{j = 1}^{J} n_{kj} = \frac{N}{K}\)가 성립한다고 하자.)
\[\begin{eqnarray*} \text{$\%$ captured response} &=& \frac{n_{kj}}{\sum_{k = 1}^{K} n_{kj}} \times 100\\ \text{cumulative $\%$ captured response} &=& \frac{\sum_{l = 1}^{k} n_{lj}}{\sum_{k = 1}^{K} n_{kj}} \times 100\\ \text{$\%$ response} &=& \frac{n_{kj}}{\sum_{j = 1}^{J} n_{kj}} \times 100\\ \text{lift} &=& \frac{n_{kj}}{\frac{1}{K} \sum_{k = 1}^{K} n_{kj}} \end{eqnarray*}\]
1,000개의 객체로 이루어진 어떤 데이터의 실제 범주별 빈도가 다음과 같다고 하자.
y_freq <- tribble(
~y, ~n,
1, 437,
2, 348,
3, 215
) %>%
mutate(y = factor(y, levels = c(1, 2, 3)))
y_freq## # A tibble: 3 x 2
## y n
## <fct> <dbl>
## 1 1 437
## 2 2 348
## 3 3 215한편, 어떤 분류모형을 사용하여 각 객체의 범주 1(특정 범주)에 대한 사후확률을 산출한 후, 전체 객체를 사후확률의 내림차순으로 정렬한 뒤 100개 객체씩 한 집단으로 구분하였다. 각 집단에 속하는 범주 1의 빈도는 다음과 같았다.
freq_within_group <- tribble(
~k, ~n,
1, 92,
2, 78,
3, 64,
4, 57,
5, 43,
6, 35,
7, 29,
8, 22,
9, 7,
10, 10
)
freq_within_group## # A tibble: 10 x 2
## k n
## <dbl> <dbl>
## 1 1 92
## 2 2 78
## 3 3 64
## 4 4 57
## 5 5 43
## 6 6 35
## 7 7 29
## 8 8 22
## 9 9 7
## 10 10 10이를 바탕으로 각 집단 별 범주 1에 대한 통계량을 산출해보자.
stat_df <- freq_within_group %>%
mutate(cum_n = cumsum(n)) %>%
mutate(
captured_response_pct = n / sum(n) * 100,
cum_captured_response_pct = cum_n / sum(n) * 100,
response_pct = n / 100 * 100,
lift = n / mean(n)
) %>%
select(-cum_n)
knitr::kable(
stat_df,
booktabs = TRUE,
align = rep('r', 6),
col.names = c('집단', '범주 1의 빈도', '% captured response',
'cum. % captured response', '% response', 'lift'),
caption = '이익도표를 위한 통계량',
digits = 2
)| 집단 | 범주 1의 빈도 | % captured response | cum. % captured response | % response | lift |
|---|---|---|---|---|---|
| 1 | 92 | 21.05 | 21.05 | 92 | 2.11 |
| 2 | 78 | 17.85 | 38.90 | 78 | 1.78 |
| 3 | 64 | 14.65 | 53.55 | 64 | 1.46 |
| 4 | 57 | 13.04 | 66.59 | 57 | 1.30 |
| 5 | 43 | 9.84 | 76.43 | 43 | 0.98 |
| 6 | 35 | 8.01 | 84.44 | 35 | 0.80 |
| 7 | 29 | 6.64 | 91.08 | 29 | 0.66 |
| 8 | 22 | 5.03 | 96.11 | 22 | 0.50 |
| 9 | 7 | 1.60 | 97.71 | 7 | 0.16 |
| 10 | 10 | 2.29 | 100.00 | 10 | 0.23 |
Table 10.2를 바탕으로 네 가지 이익도표를 작성해보자.
stat_df %>%
gather(key = "stat", value = "value",
captured_response_pct:lift) %>%
ggplot(aes(x = k, y = value)) +
geom_point() +
geom_line() +
facet_wrap(vars(stat), nrow = 2, ncol = 2, scales = "free_y",
labeller = as_labeller(
c("captured_response_pct" = "% captured response",
"cum_captured_response_pct" = "cum. % captured response",
"response_pct" = "% response",
"lift" = "lift")
)) +
xlab("group") +
ylab("statistics")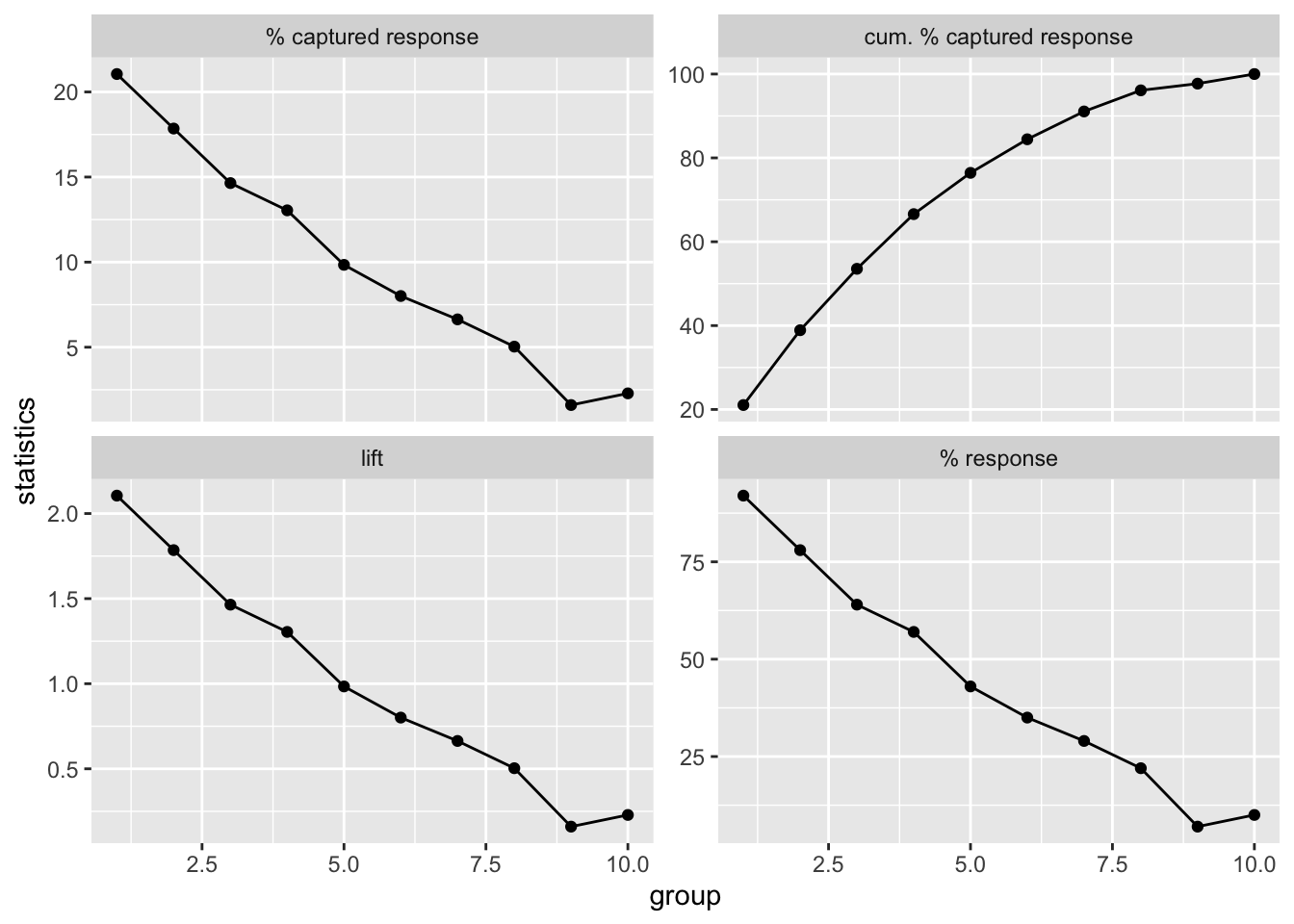
Figure 10.2: 이익도표