Chapter 8 트리기반 기법

8.1 CART 개요

CART(Classification and Regression Trees)는 Breiman et al. (1984) 에 의하여 개발된 것인데, 각 (독립)변수를 이분화(binary split)하는 과정을 반복하여 트리 형태를 형성함으로써 분류(종속변수가 범주형일 때) 또는 회귀분석(종속변수가 연속형일 때)을 수행하는 것이다. 이 때 독립변수들은 범주형 또는 연속형 모두에 적용될 수 있다. 본 장에서는 분류를 위한 목적만을 설명하도록 한다.

8.2 필요 R package 설치

본 장에서 필요한 R 패키지들은 아래와 같다.

package	version
tidyverse	1.3.1
rpart	4.1-15
rpart.plot	3.0.9

8.3 CART 트리 생성

8.3.1 기본 R 스크립트

train_df <- tibble(
  x1 = c(1,2,2,2,2,3,4,4,4,5),
  x2 = c(4,6,5,4,3,6,6,5,4,3),
  class = as.factor(c(1,1,1,2,2,1,1,2,2,2))
)

Table 8.1: 학습표본 데이터

x1	x2	class
1	4	1
2	6	1
2	5	1
2	4	2
2	3	2
3	6	1
4	6	1
4	5	2
4	4	2
5	3	2

Table 8.1와 같이 두 독립변수 x1, x2와 이분형 종속변수 class의 관측값으로 이루어진 10개의 학습표본을 train_df라는 data frame에 저장한다.

library(rpart)
library(rpart.plot)
cart.est <- rpart(
  class ~ x1 + x2
  , data = train_df
  , method = "class"
  , parms = list(split = "gini")
  , control = rpart.control(minsplit = 2
                            , minbucket = 1
                            , cp = 0
                            , xval = 0
                            , maxcompete = 0)
  )
rpart.plot(cart.est)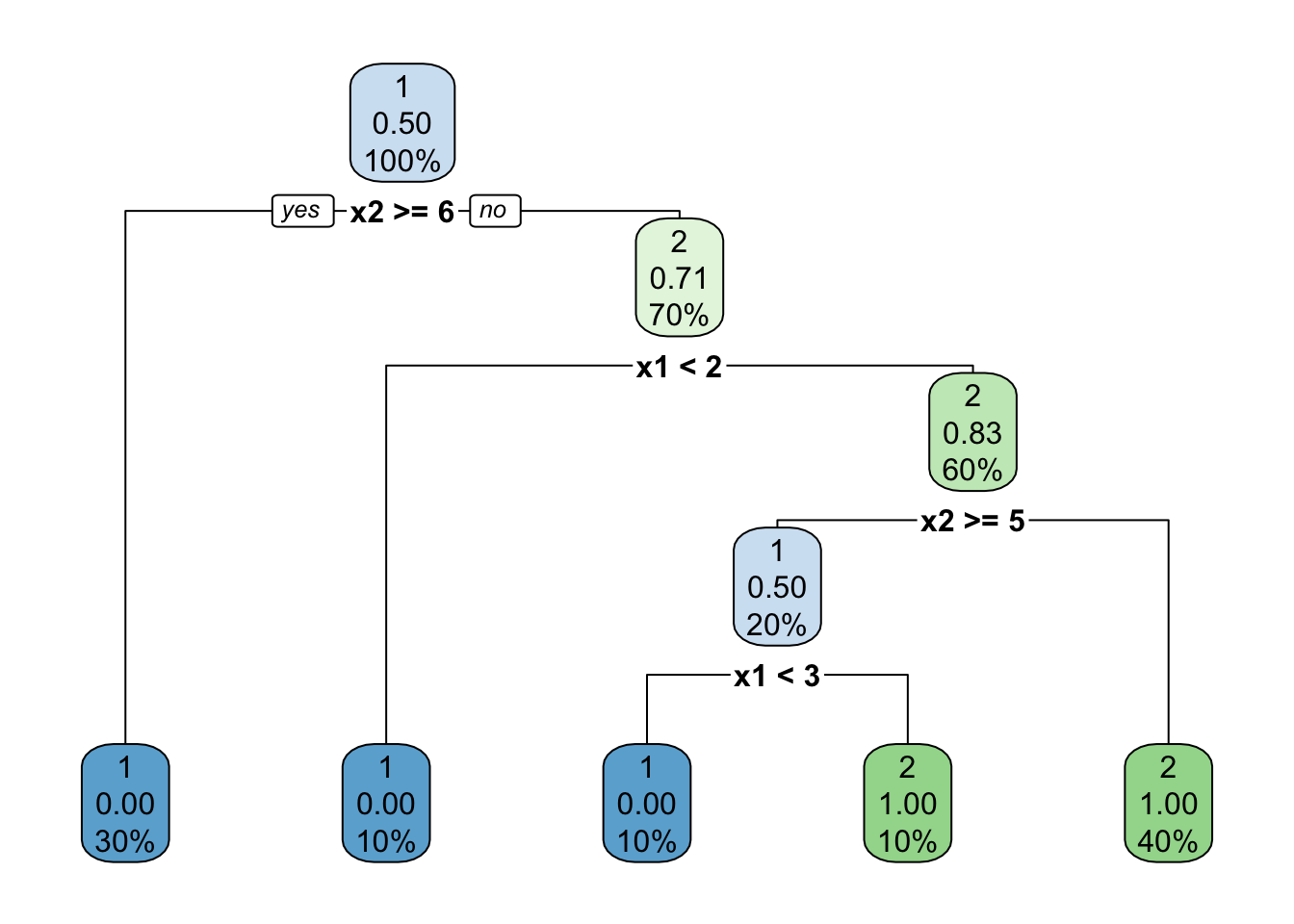

Figure 8.1: CART 트리

rpart 라는 package를 기반으로, 두 변수 x1과 x2를 이용하여 이분형 종속변수 class를 분류하는 CART 트리를 생성할 수 있으며, rpart.plot package를 이용하여 Figure 8.1과 같이 시각화할 수 있다.

8.3.2 기호 정의

본 장에서 사용될 수학적 기호는 아래와 같다.

• \(T\): 트리
• \(A(T)\): 트리 \(T\)의 최종노드의 집합
• \(J\): 범주수
• \(N\): 학습표본의 총 객체수
• \(N_j\): 범주 \(j\)에 속한 객체 수
• \(N(t)\): 노드 \(t\)에서의 객체수
• \(N_j(t)\): 노드 \(t\)에서 범주 \(j\)에 속한 객체수
• \(p(j,t)\): 임의의 객체가 범주 \(j\)와 노드 \(t\)에 속할 확률
• \(p(t)\): 임의의 객체가 노드 \(t\)에 속할 확률 \[p(t) = \sum_{j=1}^{J} p(j,t)\]
• \(p(j|t)\): 임의의 객체가 노드 \(t\)에 속할 때 범주 \(j\)에 속할 조건부 확률 \[p(j|t) = \frac{p(j,t)}{p(t)}, \quad \sum_{j=1}^{J} p(j|t) = 1\]

이 때, 각 확률은 학습표본에서 아래와 같이 추정할 수 있다. \[\begin{align} p(j,t) &\approx \frac{N_j(t)}{N}\\ p(t) &\approx \frac{N(t)}{N}\\ p(j|t) &\approx \frac{N_j(t)}{N(t)} \end{align}\]

8.3.3 노드 및 트리의 불순도

8.3.3.1 노드의 불순도

CART는 지니 지수(Gini index)를 불순도 함수로 사용한다. 총 \(J\)개의 범주별 객체비율을 \(p_1, \cdots , p_J\)라 할 때 (\(\sum_{j=1}^{J} p_j = 1\)), 지니 지수는 식 (8.1)와 같다.

\[\begin{equation} G(p_1, \cdots, p_J) = \sum_{j=1}^{J} p_j(1-p_j) = 1 - \sum_{j=1}^{J}p_j^2 \tag{8.1} \end{equation}\]

노드 \(t\)에서의 범주별 객체비율은 \(p(1|t), \cdots, p(J|t)\)이므로, 노드 \(t\)의 불순도는 식 (8.2)와 같이 산출된다.

\[\begin{equation} \begin{split} i(t) &= 1 - \sum_{j=1}^{J} p(j|t)^2\\ &\approx 1 - \sum_{j=1}^{J} \left[\frac{N_j(t)}{N(t)}\right]^2 \end{split} \tag{8.2} \end{equation}\]

8.3.3.2 트리 불순도

트리 \(T\)의 불순도는 식 (8.3)와 같이 최종노드들의 불순도의 가중평균으로 정의된다.

\[\begin{equation} I(T) = \sum_{t \in A(T)} i(t)p(t) \tag{8.3} \end{equation}\]

여기서 \[ I(t) = i(t)p(t) \] 라 하면, 다음이 성립한다. \[ I(T) = \sum_{t \in A(T)} I(t) \]

8.3.4 분지기준

뿌리 노드에서의 분지만을 살펴보기 위해 control parameter maxdepth의 값을 1으로 설정한다. 이 경우, CART 알고리즘은 뿌리노드에서의 양 갈래 분지만을 선택한 뒤 종료된다. 아래 스크립트를 이용하여 뿌리노드에서 최적분지된 트리를 얻는다.

cart.firstsplit <- rpart(class ~ x1 + x2
                  , data = train_df
                  , method = "class"
                  , parms = list(split = "gini")
                  , control = rpart.control(minsplit = 2
                                          , minbucket = 1
                                          , maxdepth = 1
                                          , cp = 0
                                          , xval = 0
                                          , maxcompete = 0
                                          )
                  )
rpart.plot(cart.firstsplit)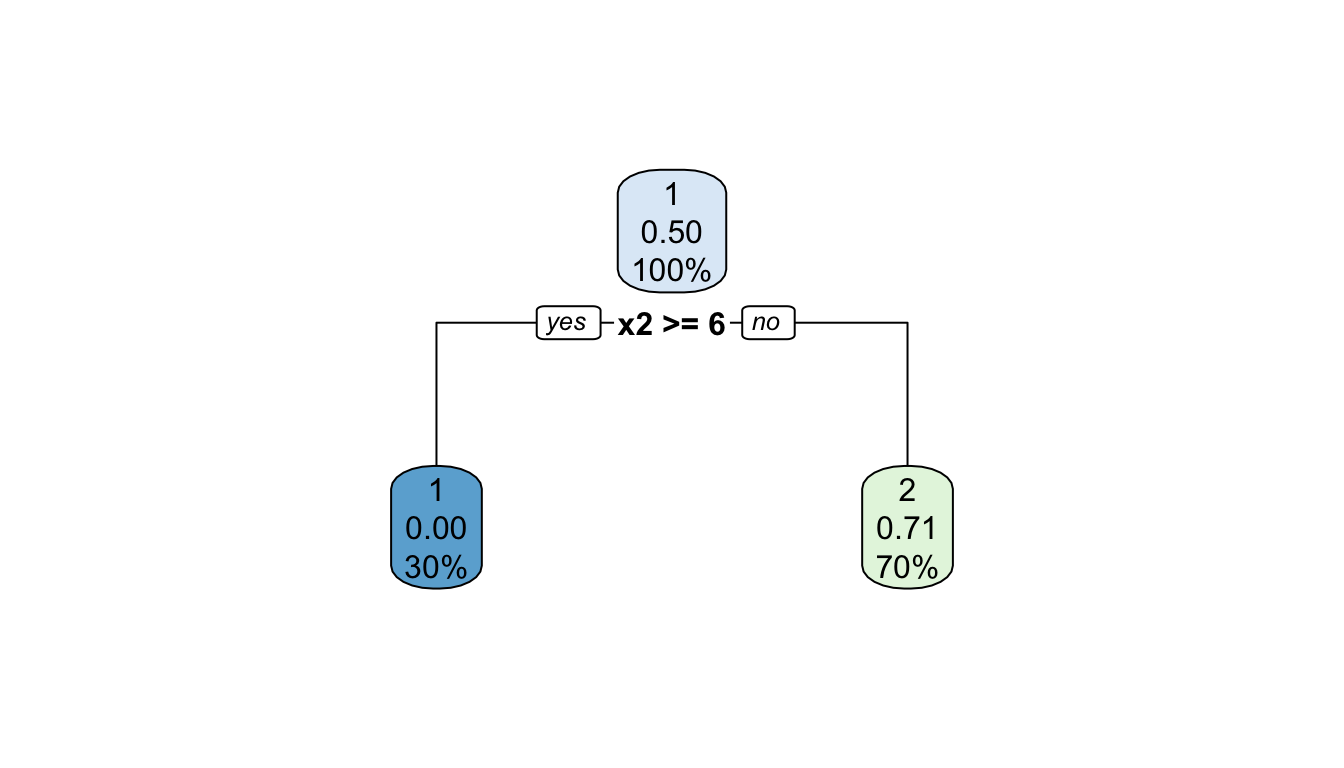

Figure 8.2: 뿌리노드 분지

또한 분지 결과 트리는 Table 8.2와 같이 frame이라는 이름의 data frame에 설명된다. 각 행 앞의 번호는 노드 인덱스 \(t\)를 나타내며, 각 열에 대한 설명은 아래와 같다.

• var: 노드 \(t\)를 분지하는 데 이용된 변수. 값이 <leaf>인 경우에는 노드 \(t\)가 최종 노드임을 나타낸다.
• n: 노드 내 객체 수 \(N(t)\)
• wt: 가중치 적용 후 객체 수 (추후 appendix에서 설명)
• dev: 오분류 객체 수
• yval: 노드 \(t\)를 대표하는 범주
• complexity: 노드 \(t\)에서 추가로 분지할 때 감소하는 relative error값; 본 분류트리 예제에서 error는 오분류율이며, 뿌리 노드의 relative error값을 1으로 한다.

Table 8.2: 뿌리노드 분지 상세 (frame)

	var	n	wt	dev	yval	complexity	ncompete	nsurrogate
1	x2	10	10	5	1	0.6	0	0
2	<leaf>	3	3	0	1	0.0	0	0
3	<leaf>	7	7	2	2	0.0	0	0

또한 frame에는 트리 내 각 노드에 속한 객체와 범주에 대한 정보를 나타내는 yval2라는 행렬이 Table 8.3와 같이 존재한다. 실제 yval2의 열의 개수는 전체 학습 대상 범주 수에 따라 달라지며, 본 예는 이분 분류 트리(범주개수 = 2)에 해당하는 열 구성을 보여준다. 각 행 앞의 번호는 노드 인덱스 \(t\)를 나타내며, 각 열에 대한 설명은 아래와 같다.

• 열1: 노드 \(t\)에서의 최적 추정 범주 \(j^*\)
• 열2: 노드 \(t\) 내 범주 class=1 객체 수 \(N_1(t)\)
• 열3: 노드 \(t\) 내 범주 class=2 객체 수 \(N_2(t)\)
• 열4: 노드 \(t\) 내 범주 class=1 관측 확률 \(p(1|t) \approx \tfrac{N_1(t)}{N(t)}\)
• 열5: 노드 \(t\) 내 범주 class=2 관측 확률 \(p(2|t) \approx \tfrac{N_2(t)}{N(t)}\)
• nodeprob: 노드 \(t\) 확률 \(p(t) \approx \tfrac{N(t)}{N}\)

## Warning: Setting row names on a tibble is deprecated.

Table 8.3: 노드 내 객체 및 범주 정보 (yval2)

	열1	열2	열3	열4	열5	nodeprob
1	1	5	5	0.50	0.50	1.0
2	1	3	0	1.00	0.00	0.3
3	2	2	5	0.29	0.71	0.7

위 CART 모델 데이터를 이용하여 트리의 불순도를 계산해보자.

우선 노드 상세 정보 행렬 yval2의 x번째 노드의 불순도(\(i(t)\))를 계산하는 함수 rpartNodeImpurity를 아래와 같이 구현한다.

rpartNodeImpurity <- function(x, yval2) {
  node_vec <- yval2[x, ]
  n.columns <- length(node_vec)
  class.prob <- node_vec[((n.columns/2)+1):(n.columns-1)]
  return(1 - sum(class.prob^2))
}

CART tree 객체의 각 leaf node에 함수 rpartNodeImpurity를 적용하여 노드 불순도 \(i(t)\)를 계산한 뒤, 노드 확률 \(p(t)\)을 이용한 가중합을 통해 트리 불순도 \(I(T)\)를 계산하는 함수 rpartImpurity를 아래와 같이 구현한다.

rpartImpurity <- function(rpart.obj) {
  leaf.nodes <- which(rpart.obj$frame$var=="<leaf>")
  node.impurity <- sapply(leaf.nodes, 
                          rpartNodeImpurity, 
                          yval2 = rpart.obj$frame$yval2)
  node.prob <- rpart.obj$frame$yval2[leaf.nodes, 'nodeprob']
  return(sum(node.prob * node.impurity))
}

위 함수를 이용하여 계산한 트리 Figure 8.1의 불순도는 0.29이다.

rpartImpurity(cart.firstsplit)

## [1] 0.2857143

분지를 추가할수록 불순도는 감소한다. 분지를 추가하기 위해서는 maxdepth라는 control parameter 값을 증가시키면 된다.

• maxdepth: 뿌리노드부터 임의의 최종노드에 도달하는 최대 가능 분지 수 (default=30)

maxdepth 파라미터의 값을 1부터 4까지 증가시키며 불순도의 변화를 살펴보자.

library(ggplot2)

tree.impurity <- sapply(c(1:4), function(depth) {
  rpart(class ~ x1 + x2
        , data = train_df
        , method = "class"
        , parms = list(split = "gini")
        , control = rpart.control(minsplit = 2
                                  , minbucket = 1
                                  , maxdepth = depth
                                  , cp = 0
                                  , xval = 0
                                  , maxcompete = 0)) %>%
  rpartImpurity()
})

tibble(maxdepth=c(1:4), impurity=tree.impurity) %>%
  ggplot(aes(x=maxdepth, y=impurity)) +
  geom_line()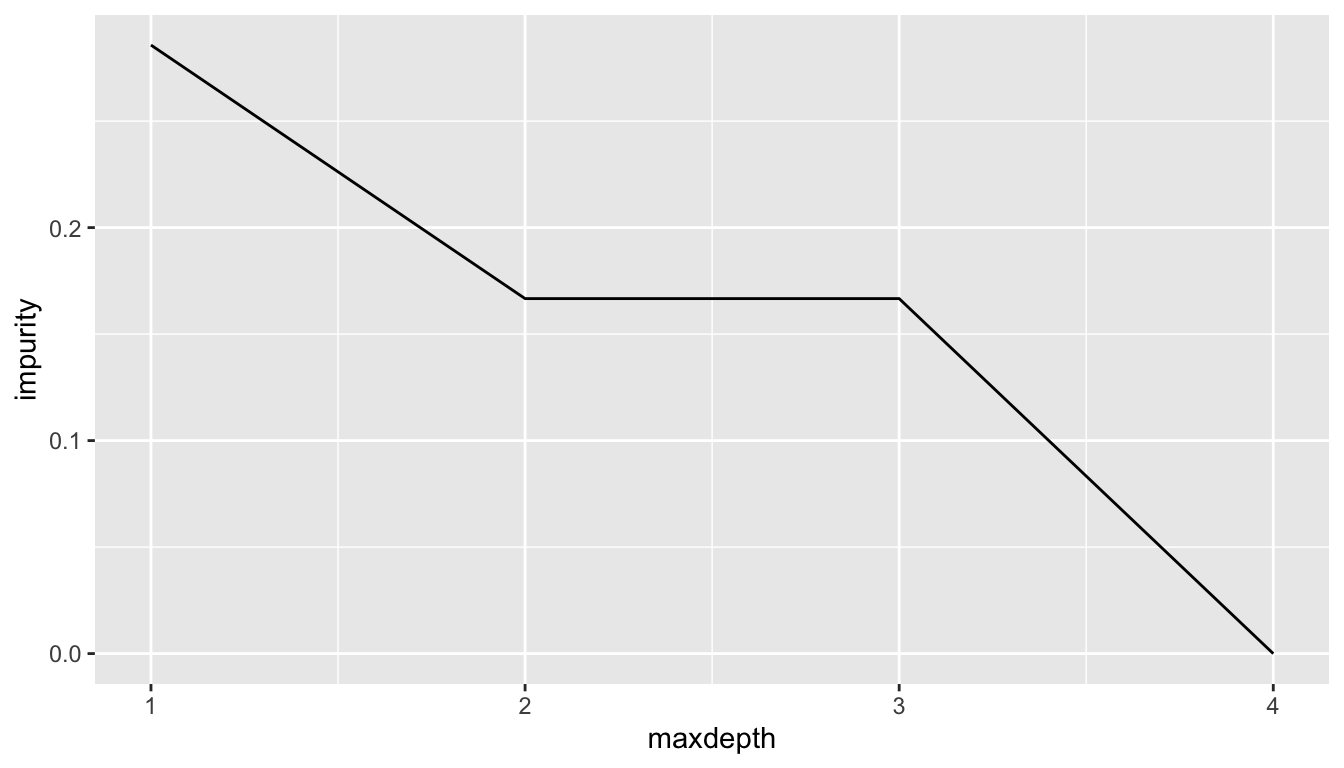

Figure 8.3: 파라미터 maxdepth값에 따른 트리불순도 변화

위 예에서, 트리의 분지가 증가함에 따라 불순도는 0.29, 0.17, 0.17, 0로 감소한다. maxdepth값이 3일 때 불순도가 감소하지 않는 이유는, 세 번째 분지 결과가 전체적인 오분류를 감소시키지 않아 rpart 함수가 해당 분지를 취소하기 때문이다. 여기에 작용하는 파라미터는 cp라는 control parameter이다.

• cp: 노드가 분지되기 위한 최소 relative error 감소치 (default = 0.01). 값이 0일 경우 최대트리를 생성한다.

위 예제에서는 cp값을 0으로 설정하여, 해당 분지가 트리 불순도를 감소시킨다 하더라도 전체 트리의 오분류를 감소시키는 데 기여하지 않는다면 시도하지 않도록 하였다.

8.4 가지치기 및 최종 트리 선정

8.4.1 가지치기

앞 장의 최대 트리 그림 8.1은 학습 데이터를 오분류 없이 완벽하게 분류하기 위해 복잡한 분류 구조를 형성하였다. 이러한 복잡한 분류 구조는 학습 데이터가 아닌 새로운 데이터에 대한 분류 정확도를 떨어뜨릴 수 있다. 이는 bias-variance tradeoff라 부르는 현상으로, 비단 분류트리 뿐 아니라 모든 데이터마이닝 방법에 일반적으로 적용된다.

분류 트리는 가지치기라는 방식을 통해, 분류 구조를 단순화함으로써 분류 트리가 새로운 데이터에도 정확한 분류를 제공하기를 추구한다. 가지치기란 트리 내 특정 내부노드를 기준으로 그 하위에 발생한 분지를 모두 제거하고, 해당 내부노드를 최종노드로 치환하는 방식이다.

Table 8.4: 최대 트리 분지 상세 (frame)

	var	n	wt	dev	yval	complexity	ncompete	nsurrogate
1	x2	10	10	5	1	0.6	0	0
2	<leaf>	3	3	0	1	0.0	0	0
3	x1	7	7	2	2	0.2	0	0
6	<leaf>	1	1	0	1	0.0	0	0
7	x2	6	6	1	2	0.1	0	0
14	x1	2	2	1	1	0.1	0	0
28	<leaf>	1	1	0	1	0.0	0	0
29	<leaf>	1	1	0	2	0.0	0	0
15	<leaf>	4	4	0	2	0.0	0	0

Table 8.4에서 생성 가능한 가지치기는 최종 노드(var값이 <leaf>)가 아닌 모든 노드(1, 3, 7, 14)에서 가능하며, 함수 snip.rpart를 이용하여 가지치기 된 트리를 생성할 수 있다. 각 내부 노드에서 가지치기된 트리들은 아래와 같이 얻어진다.

internal.node.index <- rownames(cart.est$frame)[which(cart.est$frame$var != '<leaf>')] %>%
  as.numeric()
snipped <- lapply(internal.node.index, function(x){snip.rpart(cart.est, x)})
n.trees <- length(snipped)
par(mfrow=c(2,2))
invisible(lapply(c(1:n.trees), function(x) {
  rpart.plot(snipped[[x]])}
  ))

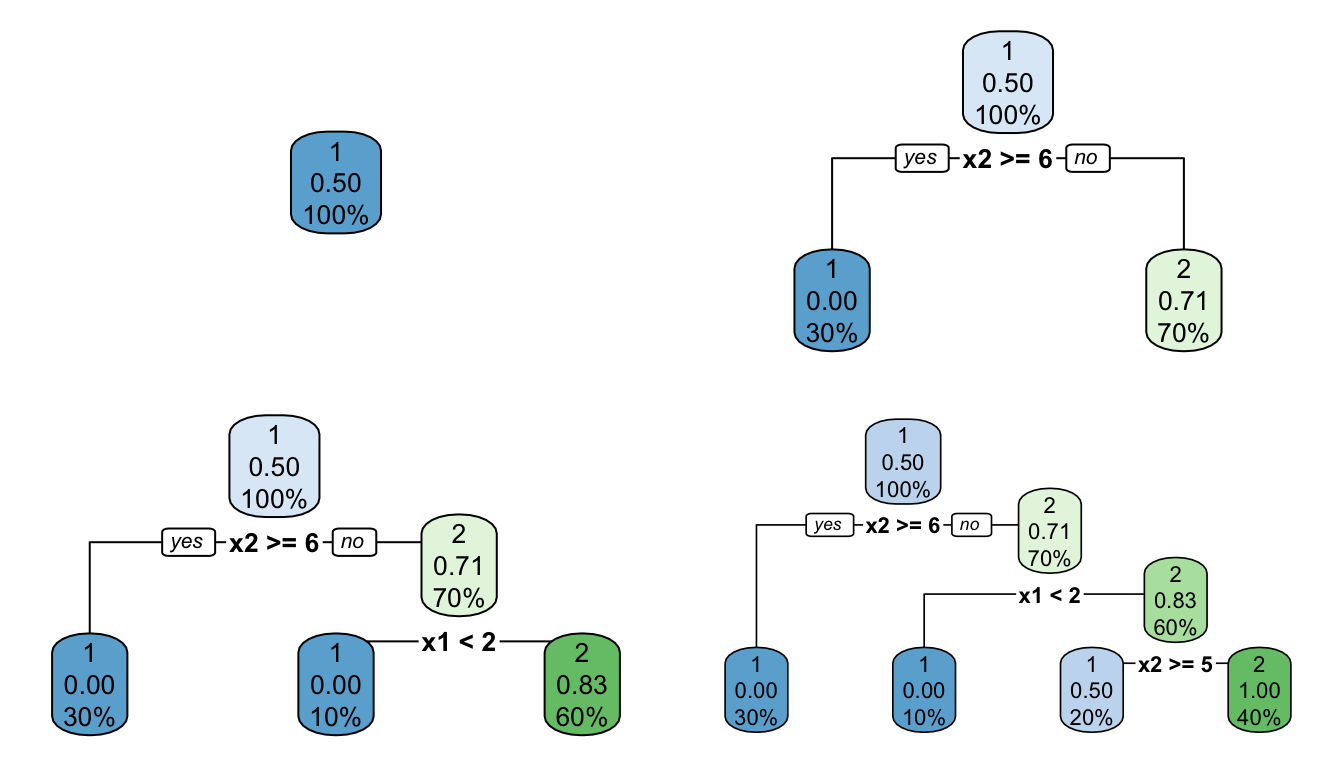
Figure 8.4: 각 내부노드 기준으로 가지치기된 트리

위 각 가지치기 후보 노드의 오분류 비용은 함수 nodeCost를 아래와 같이 구현하여 계산할 수 있다.

nodeCost <- function(node, tree) {
  node_vec <- tree$frame$yval2[as.character(node) == row.names(tree$frame), ]
  n.columns <- length(node_vec)
  class.prob.max <- max(node_vec[((n.columns/2)+1):(n.columns-1)])
  node.prob <- node_vec[n.columns]
  node.misclassification.cost <- (1-class.prob.max)*node.prob
  return(node.misclassification.cost)
}

tibble(
  pruning_node = internal.node.index,
  node_cost = sapply(internal.node.index, nodeCost, tree=cart.est)
) %>%
  knitr::kable()

pruning_node	node_cost
1	0.5
3	0.2
7	0.1
14	0.1

각 가지치기 노드에 해당하는 하부 트리의 오분류비용 및 복잡도를 구하기 위해 subtreeEval라는 함수를 아래와 같이 구현한다.

subtreeEval <- function(node, tree) {
  snipped <- snip.rpart(tree, node)$frame
  leaf.nodes <- setdiff(rownames(tree$frame[tree$frame$var=="<leaf>",]),
          rownames(snipped)) %>%
    as.numeric()

  tibble(
    pruning_node = node,
    node.cost = nodeCost(node, tree),
    subtree.cost = sapply(leaf.nodes, nodeCost, tree=tree) %>% sum(),
    subtree.size = length(leaf.nodes)
  ) %>%
  mutate(alpha = (node.cost - subtree.cost) / (subtree.size - 1))
}

각 노드에 대하여 알파값을 다음과 같이 계산할 수 있다.

df.cost <- lapply(internal.node.index, subtreeEval, tree=cart.est) %>%
  bind_rows()

Table 8.5: 내부노드 가지치기 평가 (df.cost)

pruning_node	node.cost	subtree.cost	subtree.size	alpha
1	0.5	0	5	0.12
3	0.2	0	4	0.07
7	0.1	0	3	0.05
14	0.1	0	2	0.10

위 Table 8.5 에서 최소 알파값에 해당하는 노드 7에서 가지치기를 한다.

pruned.tree.1 <- snip.rpart(cart.est,
                            df.cost$pruning_node[which.min(df.cost$alpha)])
rpart.plot(pruned.tree.1)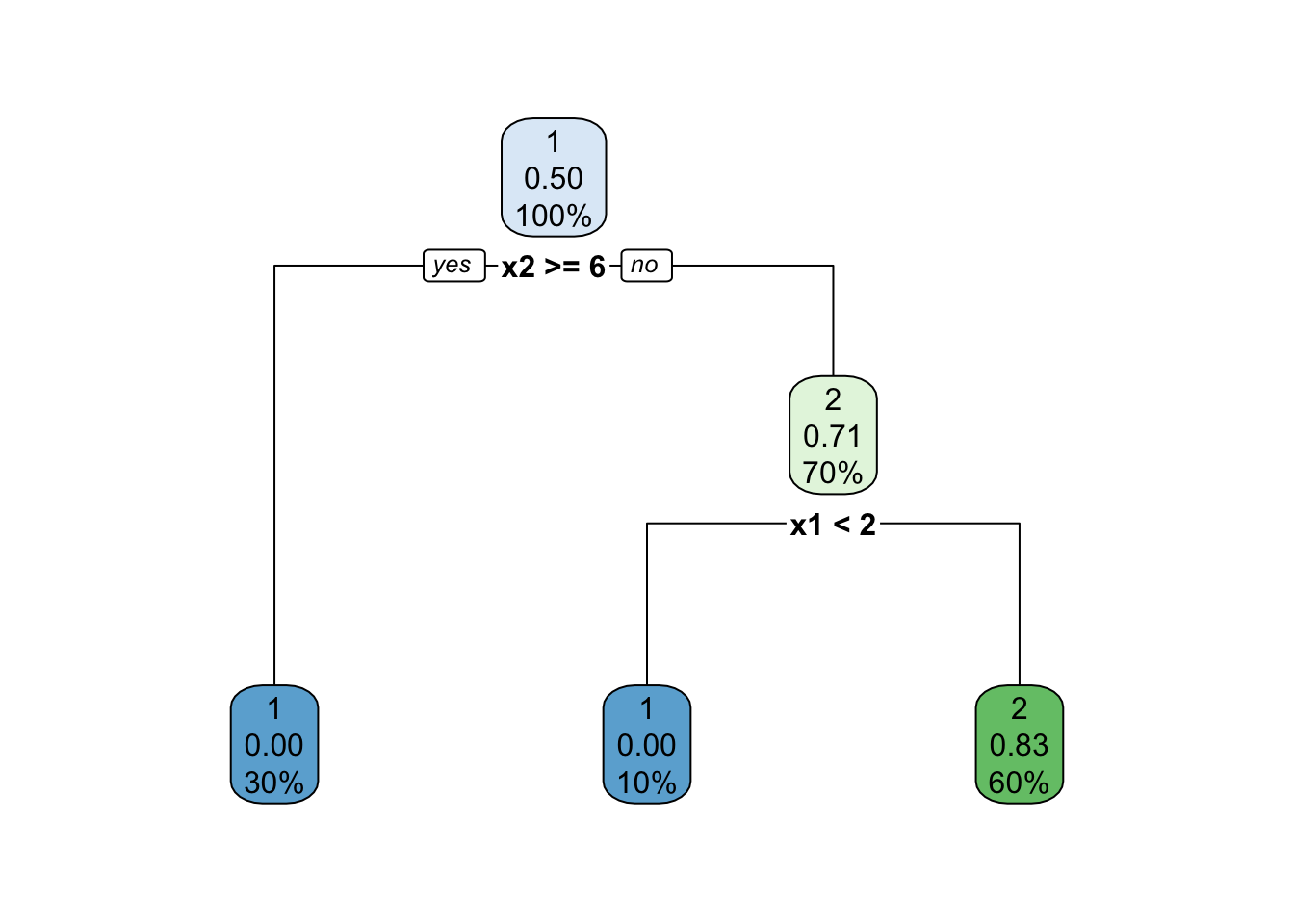

Figure 8.5: 1단계 가지치기 결과

가지치기로 형성된 트리에서 다시 각 가지치기 노드의 오분류비용, 복잡도 및 알파값을 구한다.

df.cost <- rownames(pruned.tree.1$frame)[pruned.tree.1$frame$var!="<leaf>"] %>% 
  as.numeric() %>%
  lapply(subtreeEval, tree=pruned.tree.1) %>%
  bind_rows()

knitr::kable(df.cost)

pruning_node	node.cost	subtree.cost	subtree.size	alpha
1	0.5	0.1	3	0.2
3	0.2	0.1	2	0.1

위 결과에서 다시 최소 알파값에 해당하는 노드 3에서 가지치기를 하면 아래와 같은 트리가 형성된다.

pruned.tree.2 <- snip.rpart(pruned.tree.1,
                            df.cost$pruning_node[which.min(df.cost$alpha)])
rpart.plot(pruned.tree.2)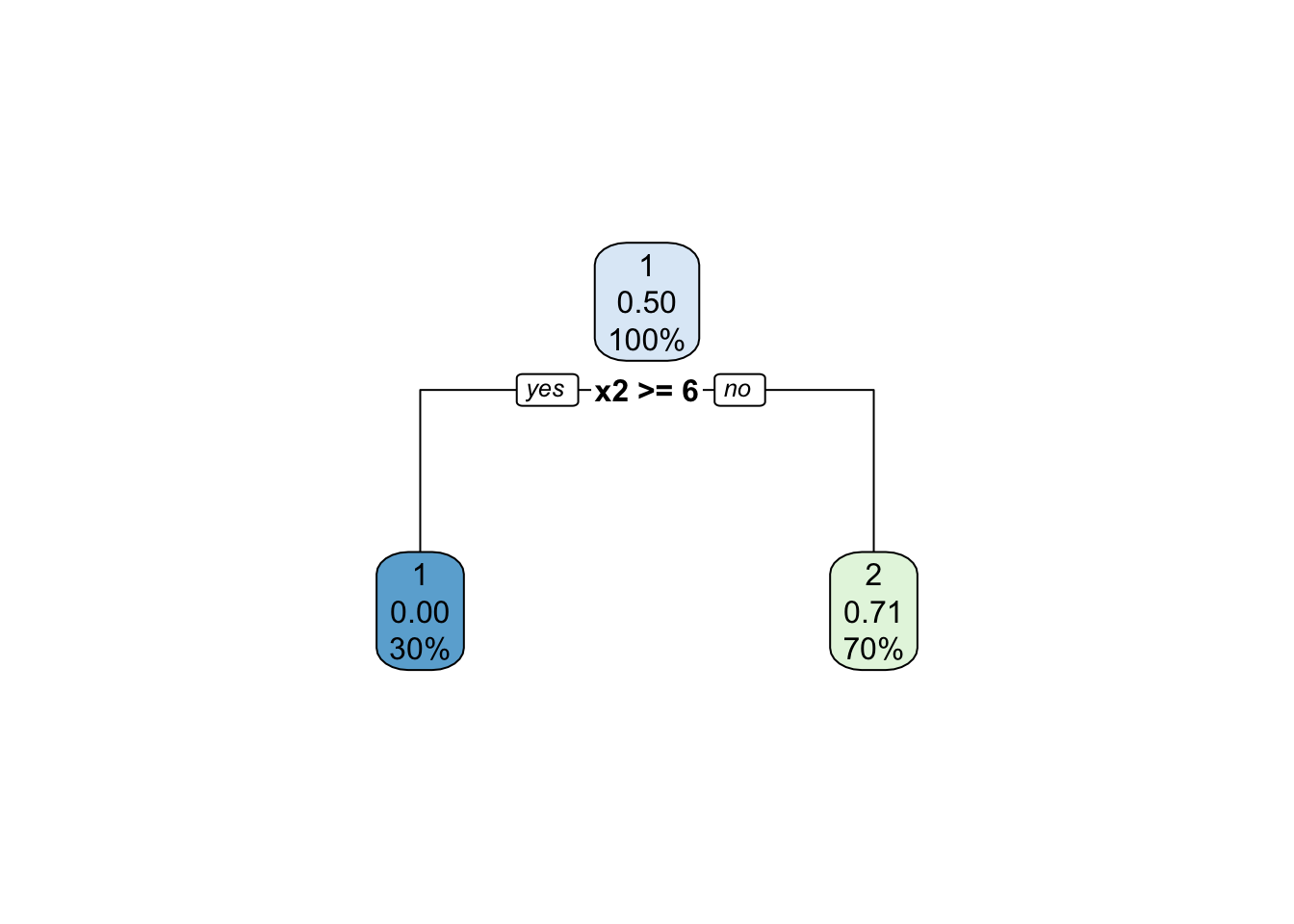

Figure 8.6: 2단계 가지치기 결과

8.4.2 최적 트리의 선정

위 가지치기 과정에서 얻는 가지친 트리들이 최종 트리의 후보가 되며, 이 중 테스트 표본에 대한 오분류율이 가장 작은 트리를 최적 트리로 선정하게 된다.

트리를 학습할 때 사용된 학습데이터 Table 8.1 외에, Table 8.6과 같은 6개의 테스트 데이터가 있다고 하자.

test_df <- tibble(
  x1 = c(1,0,3,4,2,1),
  x2 = c(5,5,4,3,7,4),
  class = factor(c(1,1,2,2,1,2), levels=c(1,2))
)

Table 8.6: 테스트 데이터

x1	x2	class
1	5	1
0	5	1
3	4	2
4	3	2
2	7	1
1	4	2

테스트 데이터에 위에서 학습된 세 개의 트리, 즉 최대 트리 cart.est와 두 개의 가지치기 트리 pruned.tree.1 & pruned.tree.2를 적용하여 각 트리가 각각의 테스트 데이터를 어떻게 분류하는지 살펴보자.

test_pred <- test_df %>%
  bind_cols(
    pred_maxtree = predict(cart.est, test_df, type="class"),
    pred_prune1 = predict(pruned.tree.1, test_df, type="class"),
    pred_prune2 = predict(pruned.tree.2, test_df, type="class")
  )

Table 8.7: 테스트 데이터에 대한 예측 결과

x1	x2	class	pred_maxtree	pred_prune1	pred_prune2
1	5	1	1	1	2
0	5	1	1	1	2
3	4	2	2	2	2
4	3	2	2	2	2
2	7	1	1	1	1
1	4	2	1	1	2

결과 Table 8.7에서 최대트리가 오분류한 테스트 표본은 1개, 첫번째 가지치기 트리가 오분류한 테스트 표본은 1개, 그리고 두 번째 가지치기 트리가 오분류한 테스트 표본은 2개이다.

위 결과를 토대로, 최적의 트리를 선정하는 과정은 아래와 같다.

1. 각각의 트리에 의해 오분류된 테스트 표본의 개수를 전체 테스트 표본의 개수로 나누어 오분류율 \(R^{ts}\)를 구한다.
2. 테스트 표본 수를 \(n_{test}\)라 할 때, 오분류의 표준편차를 아래와 같이 계산한다. \[SE = \sqrt{\frac{R^{ts}(1 - R^{ts})}{n_{test}}}\]
3. 1에서 구한 오분류율에 2에서 구한 표준편차를 더하여 \(R^{ts} + SE\)를 각 트리의 평가척도로 계산한다. 후보 트리들 중 해당 평가척도가 가장 작은 트리를 최종 트리로 선정한다.

test.summary <- test_pred %>%
  summarize(n.test = n(),
            cart.est = sum(pred_maxtree != class) / n.test,
            pruned.tree.1 = sum(pred_prune1 != class) / n.test,
            pruned.tree.2 = sum(pred_prune2 != class) / n.test) %>%
  gather("tree","R.ts",-n.test) %>%
  mutate(SE = sqrt((R.ts*(1 - R.ts))/n.test),
         score = R.ts + SE) %>%
  select(-n.test)

Table 8.8: 분류 성능

트리	오분류율(\(R^{ts}\))	표준편차(\(SE\))	척도(\(R^{ts} + SE\))
cart.est	0.17	0.15	0.32
pruned.tree.1	0.17	0.15	0.32
pruned.tree.2	0.33	0.19	0.53

위 결과, 최적 트리는 최대 트리 혹은 첫 번째 가지치기 트리가 된다.

위 절차를 임의의 데이터에 대해 수행하는 함수를 구현해보자.

rpart_learn <- function(formula, train_df, test_df) {
  # 최대 트리 생성
  max_tree <- rpart(formula
                    , data = train_df
                    , method = "class"
                    , parms = list(split = "gini")
                    , control = rpart.control(minsplit = 2
                                              , minbucket = 1
                                              , cp = 0
                                              , xval = 0
                                              , maxcompete = 0
                    )
  )
  
  # 가지치기
  curr_tree <- list()
  k <- 1
  curr_tree[[k]] <- max_tree
  while(dim(curr_tree[[k]]$frame)[1] > 1) {
    internal.node.index <- rownames(curr_tree[[k]]$frame)[which(curr_tree[[k]]$frame$var != '<leaf>')] %>%
      as.numeric()
    df.cost <- lapply(internal.node.index, subtreeEval, tree=curr_tree[[k]]) %>% bind_rows()
    curr_tree[[k + 1]] <- snip.rpart(curr_tree[[k]],
               df.cost$pruning_node[which.min(df.cost$alpha)])
    k <- k + 1
  }

  # 최적 가지치기 트리 선정
  n.test <- dim(test_df)[1]
  R.ts <- lapply(curr_tree, function(x) {
    sum(predict(x, test_df, type="class") != test_df$class) / n.test
    }) %>% unlist()
  score <- R.ts + sqrt((R.ts*(1 - R.ts))/n.test)
  return(curr_tree[[max(which(score == min(score)))]])
}

optimal_tree <- rpart_learn(class ~ x1 + x2, train_df, test_df)
rpart.plot(optimal_tree)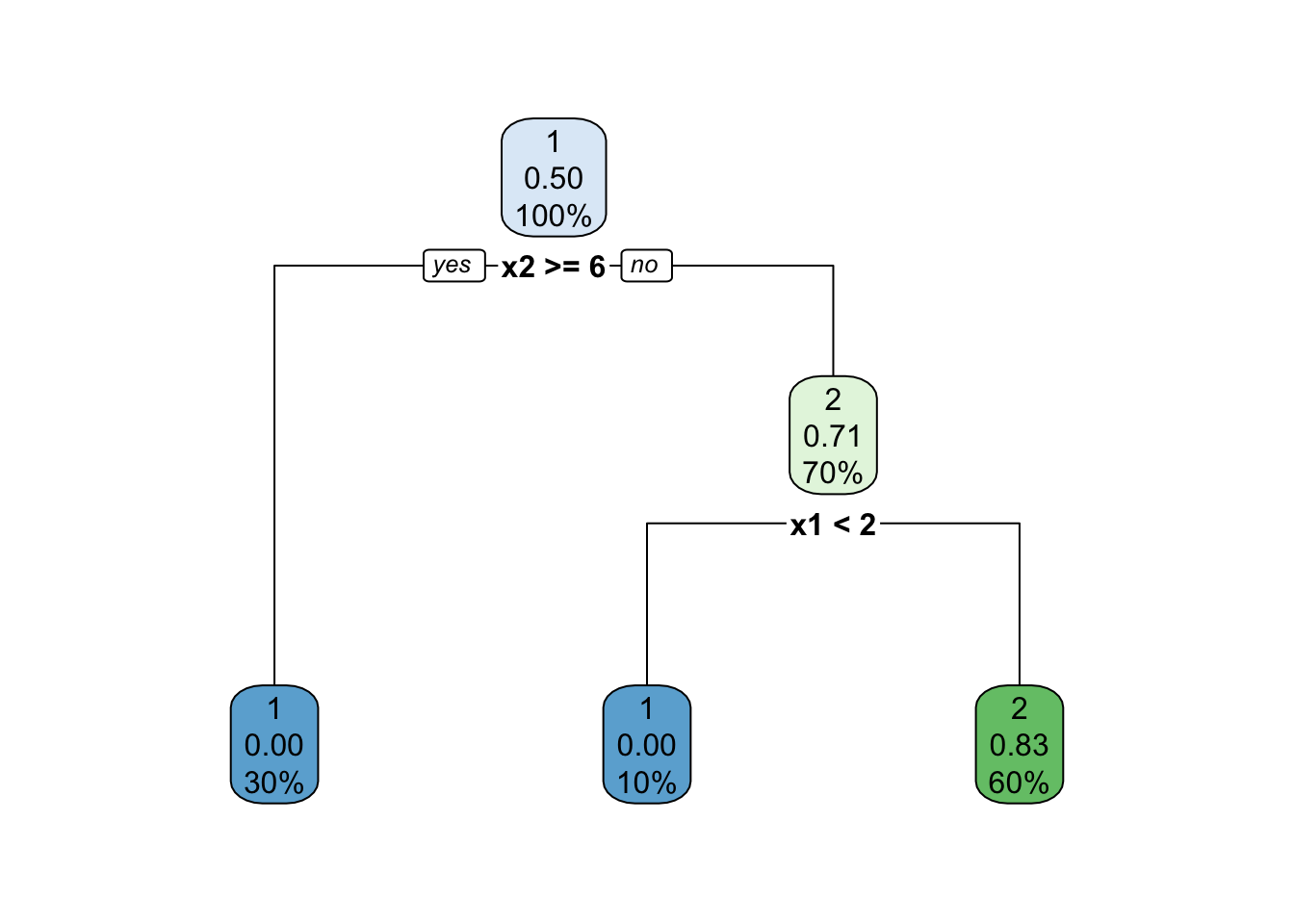

8.5 R패키지 내 분류 트리 방법

앞 장에서는 rpart의 결과를 이용하여 교재 8.2 - 8.3장의 예제를 재현해보았다. 실제로 rpart 내부의 기본 트리 방법은 교재의 예제와는 다소 다른 부분이 있다. 이 장에서는 실제 rpart 패키지의 분류 트리 방법에 대해 알아본다.

8.5.1 트리 확장

트리 내 임의의 노드 \(t\)에 대한 불순도는 아래와 같이 정의된다. \[i(t) = \sum_{j=1}^{J} f\left(p(j|t)\right)\] 여기에서 \(p(j|t)\)는 노드 \(t\) 내 전체 샘플 \(N(t)\) 중 범주 \(j\)의 샘플 \(N_j(t)\)의 비율로 추정된다. \[p(j|t) \approx \frac{N_j(t)}{N(t)}\] 또한 함수 \(f\)는 concave 함수로, \(f(0) = f(1) = 0\)의 조건을 만족시켜야 한다. rpart 에서 설정할 수 있는 함수 \(f\)의 종류에 대해서는 아래에서 좀 더 자세히 살펴보기로 한다.

트리 내 임의의 노드 \(t\)가 분지규칙 \(s\)에 따라 두 개의 노드 \(t_L\)과 \(t_R\)로 분지된다고 할 때, 불순도의 감소량은 아래와 같이 계산된다.

\[\begin{eqnarray} \Delta I(s,t) &=& I(t) - I(t_L) - I(t_R)\\ &=& p(t)i(t) - p(t_L)i(t_L) - p(t_R)i(t_R) \end{eqnarray}\]

rpart는 위 \(\Delta I(s,t)\)값이 최대가 되는 분지 기준 \(s^*\)를 찾아 노드 \(t\)를 분지하여 트리를 확장하고, 확장된 트리의 최종 노드에서 다시 최적 분지를 찾는 과정을 반복한다.

8.5.1.1 분지 함수

함수 rpart 사용 시 parms 파라미터에 split 값으로 분지 방법을 설정할 수 있다.

1. Gini index (parms=list(split=‘gini’)) 교재의 예제에 사용된 방법으로, 우선 아래와 같은 함수 \(f\)를 사용한다. \[f(p) = p(1-p)\]
2. information index (parms=list(split=‘information’)) 교재에 엔트로피 지수(Entropy index)로 설명된 지수로, 아래와 같은 함수를 사용한다. \[f(p) = -p\log(p)\]
3. user-defined function 사용자가 임의로 함수를 정의하여 사용할 수 있다. 본 장에서는 자세한 설명은 생략한다.

8.5.2 가지치기

임의의 노드 \(t\)에 대한 위험도(오분류 비용의 기대치)는 아래와 같이 계산된다. \[r(t) = \sum_{j \neq \tau(t)} p(j|t)C\left(\tau(t)|j\right)\] 여기에서 함수 \(C(i|j)\)는 범주 \(j\)에 속하는 객체를 범주 \(i\)로 분류할 때의 오분류 비용이며, \(\tau(t)\)는 노드 \(t\) 내의 오분류 비용을 최소화하도록 노드 \(t\)에 지정된 범주값이다.

rpart의 오분류 비용 \(C(i|j)\)의 기본값은 \[C(i|j) = \begin{cases} 1, & \text{ if } i \neq j\\ 0, & \text{ if } i = j \end{cases} \] 으로 설정되어 있으며, parms 파라미터에 loss 값으로 오분류 비용 \(C(i|j)\)를 재설정할 수 있다. 본 장에서는 기본값을 사용하도록 하자.

\(A(T)\)를 트리 \(T\)의 최종 노드의 집합이라 정의하고, 트리의 최종 노드의 개수를 \(|T|\)라 할 때, 트리 \(T\)의 위험도 \(R(T)\)는 아래와 같이 정의된다. \[R(T) = \sum_{t \in A(T)} p(t)r(t)\]

복잡도 계수(complexity parameter) \(\alpha \in [0, \infty)\)를 이용하여, 트리의 비용-복합도 척도를 다음과 같이 정의한다. \[R_\alpha(T) = R(T) + \alpha|T|\] 이 때, 임의의 계수 \(\alpha\)에 대해 비용 \(R_\alpha(T)\)가 최소가 되게하는 가지치기 트리를 \(T_\alpha\)라 하면, 아래와 같은 관계들이 성립한다.

• \(T_0\): 최대 트리
• \(T_\infty\): 뿌리 노드 트리 (분지 없음)
• \(\alpha > \beta\)일 때, \(T_\alpha\)는 \(T_\beta\)와 동일하거나 혹은 \(T_\beta\)에서 가지치기된 트리이다.

8.5.3 파라미터값 결정

함수 rpart를 사용할 때 여러가지 사용자 정의 파라미터값을 설정할 수 있으며, 그 파라미터 값에 따라 생성되는 트리의 결과가 달라진다. 대표적인 파라미터 값으로는 아래와 같은 것들이 있다.

• minsplit: 분지를 시도하기 위해 필요한 노드 내 최소 관측객체 수 (default=20)
• cp: 노드가 분지되기 위한 최소 relative error 감소치 (default = 0.01). 값이 0일 경우 최대트리를 생성한다.
• maxdepth: 뿌리노드부터 임의의 최종노드에 도달하는 최대 가능 분지 수 (default=30)

References

Breiman, Leo, Jerome Friedman, Charles J Stone, and Richard A Olshen. 1984. Classification and Regression Trees. CRC press.