Chapter 3 주성분분석
3.1 필요 R 패키지 설치
본 장에서 필요한 R 패키지들은 아래와 같다.
| package | version |
|---|---|
| tidyverse | 1.3.1 |
| stats | 4.1.3 |
| broom | 0.7.8 |
| Matrix | 1.3-4 |
| nipals | 0.7 |
3.2 행렬의 분해
3.2.1 기본 R 스트립트
아래 Table 3.1는 국내 18개 증권회사의 주요 재무제표를 나열한 것이다.
train_df <- tribble(
~company, ~roa, ~roe, ~bis, ~de_ratio, ~turnover,
"SK증권", 2.43, 11.10, 18.46, 441.67, 0.90,
"교보증권", 3.09, 9.95, 29.46, 239.43, 0.90,
"대신증권", 2.22, 6.86, 28.62, 249.36, 0.69,
"대우증권", 5.76, 23.19, 23.47, 326.09, 1.43,
"동부증권", 1.60, 5.64, 25.64, 289.98, 1.42,
"메리츠증권", 3.53, 10.64, 32.25, 210.10, 1.17,
"미래에셋증권", 4.26, 15.56, 24.40, 309.78, 0.81,
"부국증권", 3.86, 5.50, 70.74, 41.36, 0.81,
"브릿지증권", 4.09, 6.44, 64.38, 55.32, 0.32,
"삼성증권", 2.73, 10.68, 24.41, 309.59, 0.64,
"서울증권", 2.03, 4.50, 42.53, 135.12, 0.59,
"신영증권", 1.96, 8.92, 18.48, 441.19, 1.07,
"신흥증권", 3.25, 7.96, 40.42, 147.41, 1.19,
"우리투자증권", 2.01, 10.28, 17.46, 472.78, 1.25,
"유화증권", 2.28, 3.65, 63.71, 56.96, 0.12,
"한양증권", 4.51, 7.50, 63.52, 57.44, 0.80,
"한화증권", 3.29, 12.37, 24.47, 308.63, 0.57,
"현대증권", 1.73, 7.57, 19.59, 410.45, 1.19
)
knitr::kable(
train_df, booktabs = TRUE,
align = rep("r", ncol(train_df)),
col.names = c(
"회사",
"총자본 순이익율 ($x_1$)",
"자기자본 순이익율 ($x_2$)",
"자기자본비율 ($x_3$)",
"부채비율 ($x_4$)",
"자기자본 회전율 ($x_5$)"
),
caption = "국내 증권회사의 주요 재무제표"
)| 회사 | 총자본 순이익율 (\(x_1\)) | 자기자본 순이익율 (\(x_2\)) | 자기자본비율 (\(x_3\)) | 부채비율 (\(x_4\)) | 자기자본 회전율 (\(x_5\)) |
|---|---|---|---|---|---|
| SK증권 | 2.43 | 11.10 | 18.46 | 441.67 | 0.90 |
| 교보증권 | 3.09 | 9.95 | 29.46 | 239.43 | 0.90 |
| 대신증권 | 2.22 | 6.86 | 28.62 | 249.36 | 0.69 |
| 대우증권 | 5.76 | 23.19 | 23.47 | 326.09 | 1.43 |
| 동부증권 | 1.60 | 5.64 | 25.64 | 289.98 | 1.42 |
| 메리츠증권 | 3.53 | 10.64 | 32.25 | 210.10 | 1.17 |
| 미래에셋증권 | 4.26 | 15.56 | 24.40 | 309.78 | 0.81 |
| 부국증권 | 3.86 | 5.50 | 70.74 | 41.36 | 0.81 |
| 브릿지증권 | 4.09 | 6.44 | 64.38 | 55.32 | 0.32 |
| 삼성증권 | 2.73 | 10.68 | 24.41 | 309.59 | 0.64 |
| 서울증권 | 2.03 | 4.50 | 42.53 | 135.12 | 0.59 |
| 신영증권 | 1.96 | 8.92 | 18.48 | 441.19 | 1.07 |
| 신흥증권 | 3.25 | 7.96 | 40.42 | 147.41 | 1.19 |
| 우리투자증권 | 2.01 | 10.28 | 17.46 | 472.78 | 1.25 |
| 유화증권 | 2.28 | 3.65 | 63.71 | 56.96 | 0.12 |
| 한양증권 | 4.51 | 7.50 | 63.52 | 57.44 | 0.80 |
| 한화증권 | 3.29 | 12.37 | 24.47 | 308.63 | 0.57 |
| 현대증권 | 1.73 | 7.57 | 19.59 | 410.45 | 1.19 |
이에 대하여 R 기본 stats 패키지 내의 prcomp 함수를 이용하여 주성분 분석을 수행할 수 있다.
pca_fit <- prcomp(~ roa + roe + bis + de_ratio + turnover,
data = train_df, scale = TRUE)
pca_fit## Standard deviations (1, .., p=5):
## [1] 1.6617648 1.2671437 0.7419994 0.2531070 0.1351235
##
## Rotation (n x k) = (5 x 5):
## PC1 PC2 PC3
## roa 0.07608427 -0.77966993 0.0008915975
## roe -0.39463007 -0.56541218 -0.2953216494
## bis 0.56970191 -0.16228156 0.2412221065
## de_ratio -0.55982770 0.19654293 -0.2565972887
## turnover -0.44778451 -0.08636803 0.8881182665
## PC4 PC5
## roa -0.140755404 0.60540325
## roe 0.117644166 -0.65078503
## bis -0.637721889 -0.42921686
## de_ratio -0.748094314 0.14992183
## turnover -0.003668418 -0.05711464summary(pca_fit)## Importance of components:
## PC1 PC2 PC3 PC4
## Standard deviation 1.6618 1.2671 0.7420 0.25311
## Proportion of Variance 0.5523 0.3211 0.1101 0.01281
## Cumulative Proportion 0.5523 0.8734 0.9835 0.99635
## PC5
## Standard deviation 0.13512
## Proportion of Variance 0.00365
## Cumulative Proportion 1.00000각 주성분에 대한 고유값을 스크리 도표로 나타내면 아래 Figure 3.1
screeplot(pca_fit, main = NULL)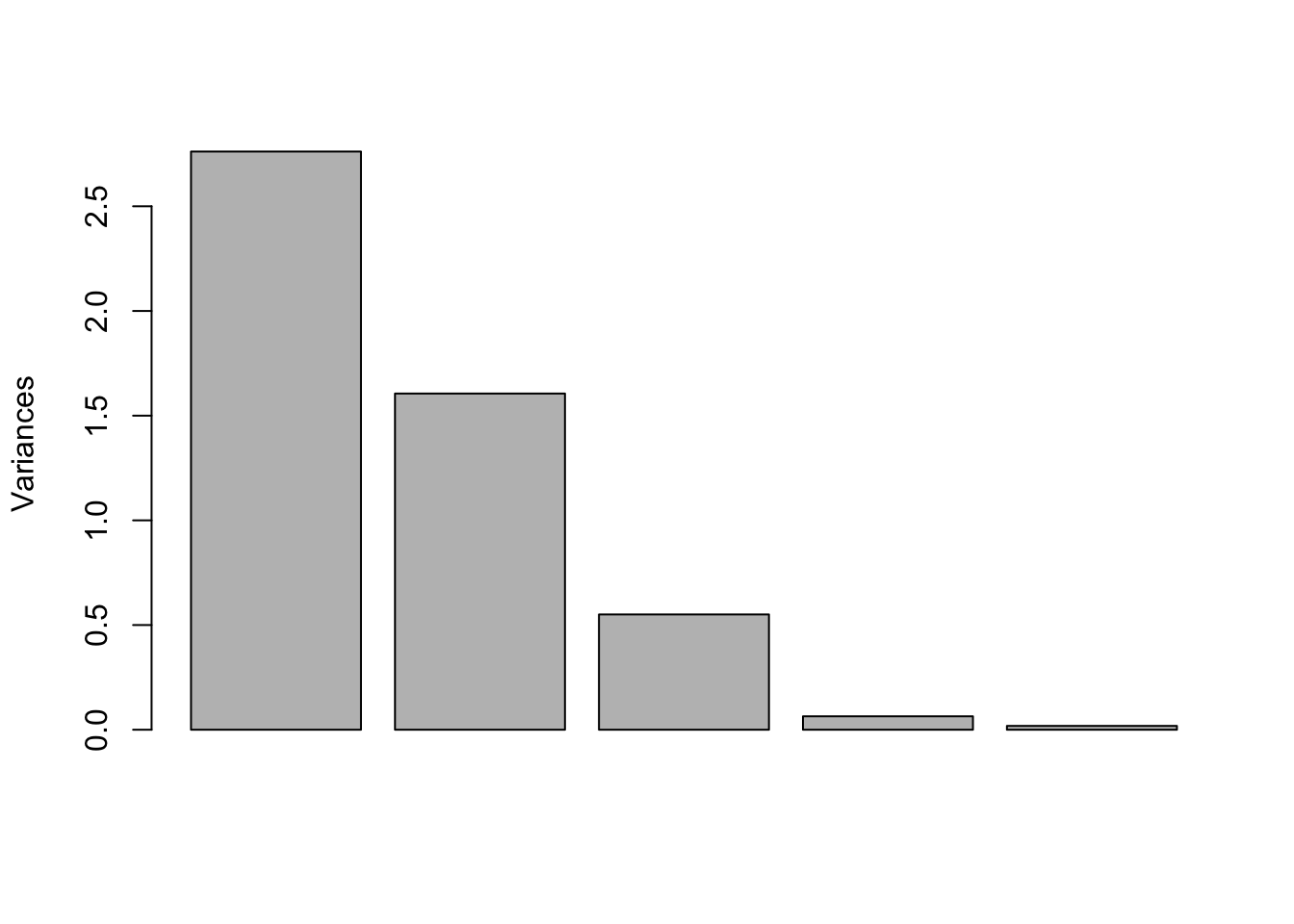
Figure 3.1: 고유치 스크리 도표
3.2.2 변수의 변동과 제곱합
총 \(k\)개의 독립변수가 있고 각 독립변수에 대하여 \(n\)개의 관측치가 있다고 하자. 이 때, \(x_{ij}\)를 \(j\)번째 독립변수에 대한 \(i\)번째 관측치라 하자. 즉, 관측데이터는 아래와 같은 행렬로 표현할 수 있다.
\[\begin{equation*} \mathbf{X} = \left[ \begin{array}{c c c c} x_{11} & x_{12} & \cdots & x_{1k}\\ x_{21} & x_{22} & \cdots & x_{2k}\\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{nk} \end{array} \right] \end{equation*}\]
주성분분석에서는 통상 원데이터를 그대로 사용하지 않고 적절한 변환을 취하는데, 주로 평균조정(mean-centered) 데이터를 이용한다. 이는 아래와 같이 독립변수에 대하여 표본평균을 뺌으로써 조정된 변수의 평균이 0이 되도록 하는 것이다.
\[\begin{equation} x_{ij} \leftarrow x_{ij} - \frac{1}{n} \sum_{l = 1}^{n} x_{lj} \tag{3.1} \end{equation}\]
이후에 별도의 언급이 없는 한, 행렬 \(\mathbf{X}\) 및 변수값 \(x_{ij}\)는 식 (3.1)을 이용하여 평균조정된 것으로 가정한다.
이 밖에도 다른 변환이 사용되는 경우가 있는데, 특히 단위 등이 서로 상이할 경우에는 평균조정 이후 추가로 각 변수의 분산이 1이 되도록 분산조정을 한다.
\[\begin{equation*} z_{ij} \leftarrow \frac{x_{ij}}{\sqrt{\frac{1}{n - 1} \sum_{l =1}^{n} x_{lj}^2}} \tag{3.2} \end{equation*}\]
이 때, 식 (3.2)에서 분모 부분은 변수의 표본 표준편차로 \(s_j\)로 표현된다.
\[\begin{equation*} s_{j} = \sqrt{\frac{1}{n - 1} \sum_{l =1}^{n} x_{lj}^2} \end{equation*}\]
이후 분산조정을 이용하는 경우 행렬 \(\mathbf{Z}\) 및 변수값 \(z_{ij}\)로 표현한다.
\[\begin{equation*} \mathbf{Z} = \left[ \begin{array}{c c c c} z_{11} & z_{12} & \cdots & z_{1k}\\ z_{21} & z_{22} & \cdots & z_{2k}\\ \vdots & \vdots & \ddots & \vdots \\ z_{n1} & z_{n2} & \cdots & z_{nk} \end{array} \right] \end{equation*}\]
변수벡터 \(\mathbf{x}_j = [x_{1j} \, x_{2j} \, \cdots \, x_{nj}]^\top\)에 대한 제곱합의 정의는 아래와 같다.
\[\begin{equation} SS(\mathbf{x}_j) = \mathbf{x}_j^\top \mathbf{x}_j = \sum_{i = 1}^{n} x_{ij}^2 \end{equation}\]
따라서, 평균조정된 변수에 대해 제곱합고 표본분산은 다음과 같은 관계가 있다.
\[\begin{equation*} SS(\mathbf{x}_j) = (n - 1) s_j^2 \end{equation*}\]
변수행렬 \(\mathbf{X}\)에 대한 제곱합은 각 변수들의 제곱합의 총합(총변동)으로 정의된다.
\[\begin{equation} SS(\mathbf{X}) = \sum_{j = 1}^{k} SS(\mathbf{x}_j) = \sum_{j = 1}^{k} \sum_{i = 1}^{n} x_{ij}^2 \end{equation}\]
Table 3.1 데이터에 대하여 각 변수의 제곱합을 계산해보자.
train_df %>%
mutate_if(is.numeric, function(x) x - mean(x)) %>% # mean-centering
summarize_if(is.numeric, function(x) sum(x ^ 2)) # sum of squares by variable## # A tibble: 1 x 5
## roa roe bis de_ratio turnover
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 21.9 355. 5591. 347817. 2.23전체 데이터 행렬에 대한 제곱합은 아래와 같다.
train_df %>%
mutate_if(is.numeric, function(x) x - mean(x)) %>% # mean-centering
summarize_if(is.numeric, function(x) sum(x ^ 2)) %>% # sum of squares by variable
{sum(.)}## [1] 353786.6위 결과에서 부채비율(de_ratio)의 변동이 총변동의 대부분을 차지하고, 자기자본 회전율(turnover)이 총변동에 미치는 영향은 미미한데, 이는 각 변수들이 측정하는 값의 분포(범위)가 크게 다르기 때문이다. 이러한 경우, 일반적으로 분산조정을 추가로 적용한 뒤 주성분분석을 수행한다.
standardized_df <- train_df %>%
mutate_if(is.numeric, function(x) x - mean(x)) %>% # mean-centering
mutate_if(is.numeric, function(x) x / sd(x)) # scalingstandardized_df## # A tibble: 18 x 6
## company roa roe bis de_ratio turnover
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 SK증권 -0.533 0.383 -0.918 1.34 0.0507
## 2 교보증권 0.0484 0.131 -0.312 -0.0749 0.0507
## 3 대신증권 -0.718 -0.545 -0.358 -0.00551 -0.530
## 4 대우증권 2.40 3.03 -0.642 0.531 1.52
## 5 동부증권 -1.26 -0.812 -0.522 0.278 1.49
## 6 메리츠증권 0.436 0.282 -0.158 -0.280 0.797
## 7 미래에셋증권 1.08 1.36 -0.591 0.417 -0.198
## 8 부국증권 0.726 -0.843 1.96 -1.46 -0.198
## 9 브릿지증권 0.929 -0.637 1.61 -1.36 -1.55
## 10 삼성증권 -0.269 0.291 -0.590 0.416 -0.668
## 11 서울증권 -0.885 -1.06 0.409 -0.804 -0.806
## 12 신영증권 -0.947 -0.0942 -0.917 1.34 0.521
## 13 신흥증권 0.189 -0.304 0.293 -0.718 0.852
## 14 우리투자증권 -0.903 0.203 -0.973 1.56 1.02
## 15 유화증권 -0.665 -1.25 1.58 -1.35 -2.11
## 16 한양증권 1.30 -0.405 1.57 -1.35 -0.226
## 17 한화증권 0.225 0.661 -0.587 0.409 -0.861
## 18 현대증권 -1.15 -0.390 -0.856 1.12 0.852분산조정 이후의 각 변수의 제곱합은 모두 \(n - 1\)이 되는데, 이는 각 변수의 표본분산이 모두 1로 조정되기 때문이다.
standardized_df %>%
summarize_if(is.numeric, function(x) sum(x ^ 2)) # sum of squares by variable## # A tibble: 1 x 5
## roa roe bis de_ratio turnover
## <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 17 17 17 17 17따라서, 분산조정 이후 총변동은 아래와 같다.
total_ss <- standardized_df %>%
summarize_if(is.numeric, function(x) sum(x ^ 2)) %>% # sum of squares by variable
{sum(.)}
total_ss## [1] 853.2.3 주성분의 이해 및 행렬의 분해
주성분분석은 원래의 변수들의 선형조합으로 서로 직교하는 새로운 변수들을 생성하는 것이라 할 수 있다. 이 때, 원래 변수의 수 \(k\)보다 작은 \(A\)개의 새로운 변수들이 원 데이터 행렬 \(\mathbf{X}\) 총변동의 대부분을 설명한다고 하면, 해당 새로운 변수들만을 사용하여 여러 가지 분석을 대신할 수 있다는 것이 주성분분석의 개념이라 하겠다.
새로운 변수 \(\mathbf{t}_1, \cdots, \mathbf{t}_A\)들은 다음과 같은 형태로 표현된다.
\[\begin{equation} \mathbf{t}_a = \sum_{j = 1}^{k} p_{aj} \mathbf{x}_j, \, a = 1, \cdots, A \end{equation}\]
결과적으로 주성분분석은 위와 같이 표현되는 새로운 변수를 만들 때 필요한 계수 \(p_{aj}\)를 구하는 것이라 할 수 있겠다. \(\mathbf{t}_1\)이 \(\mathbf{X}\)의 변동을 가장 많이 설명하도록, \(\mathbf{t}_2\)는 \(\mathbf{t}_1\)이 설명하지 못한 변동을 가장 많이 설명하도록 하는 방식으로 \(A\)개의 새로운 변수를 순차적으로 찾아내는 것이 기본적인 원리이다.
Table 3.1 데이터에 대하여 분산조정을 적용한 후 아래 식을 이용하여 새로운 변수를 도출해보자.
\[ t_1 = 0.07608427 \times roa - 0.39463007 \times roe + 0.56970191 \times bis - 0.55982770 \times de\_ratio - 0.44778451 \times turnover \]
new_df <- standardized_df %>%
mutate(t_1 = 0.07608427 * roa - 0.39463007 * roe
+ 0.56970191 * bis - 0.55982770 * de_ratio
- 0.44778451 * turnover) %>%
select(company, t_1) # new variableprint(new_df)## # A tibble: 18 x 2
## company t_1
## <chr> <dbl>
## 1 SK증권 -1.49
## 2 교보증권 -0.206
## 3 대신증권 0.197
## 4 대우증권 -2.35
## 5 동부증권 -0.895
## 6 메리츠증권 -0.368
## 7 미래에셋증권 -0.935
## 8 부국증권 2.41
## 9 브릿지증권 2.70
## 10 삼성증권 -0.405
## 11 서울증권 1.40
## 12 신영증권 -1.54
## 13 신흥증권 0.322
## 14 우리투자증권 -2.03
## 15 유화증권 3.04
## 16 한양증권 2.01
## 17 한화증권 -0.421
## 18 현대증권 -1.43이 때, 새로운 변수 \(\mathbf{t}_1\)는 분산조정된 행렬 \(\mathbf{Z}\)의 총변동의 약 55%를 설명한다.
t1_ss <- new_df %>%
summarize_if(is.numeric, function(x) sum(x ^ 2))
t1_ss / total_ss## t_1
## 1 0.5522924위 새로운 변수 \(\mathbf{t}_1\)는 실제로 행렬 \(\mathbf{Z}\)로부터 얻어지는 첫 번째 주성분이며, 행렬 \(\mathbf{Z}\)의 변동에 가장 많이 기여하는 하나의 선형조합이다.
행렬 \(\mathbf{Z}\)(혹은 \(\mathbf{X}\))로부터 주성분을 얻는 방법은 여러 가지가 있으며, 아래에서 하나씩 설명하기로 한다.
3.2.4 특이치분해 (Singular Value Decomposition)
분산조정된 \(\mathbf{Z}\)에 대해 주성분분석을 수행한다고 가정하자. 분산조정을 하지 않고 주성분분석을 수행하는 경우 아래 행렬 \(\mathbf{Z}\) 대신 \(\mathbf{X}\)를 사용하면 된다.
임의의 \((n \times k)\) 행렬 \(\mathbf{Z}\)는 다음과 같이 분해된다.
\[\begin{equation} \mathbf{Z} = \mathbf{U} \mathbf{D} \mathbf{V}^\top \tag{3.3} \end{equation}\]
이 때, \(r = \min\{n, k\}\)라 할 때,
- \(\mathbf{U}\): \((n \times r)\) 직교 (orthogonal) 행렬
- \(\mathbf{D}\): \((r \times r)\) 대각 (diagonal) 행렬. rank 수만큼의 비음 대각원소들을 가지며, 각 비음 대각원소를 힝렬 \(\mathbf{Z}\)의 특이치(singular value)라 하고, 특이치가 내림차순으로 정렬되는 형태로 행렬이 구성된다.
- \(\mathbf{V}\): \((k \times r)\) 직교 (orthogonal) 행렬
아래와 같이, R 함수 svd를 이용하여 분해한 행렬들을 곱한 결과가 원래 행렬 \(\mathbf{Z}\)와 동일함을 확인할 수 있다.
Z <- as.matrix(standardized_df[, -1])
svd_Z <- svd(Z)
Z_rec <- svd_Z$u %*% diag(svd_Z$d) %*% t(svd_Z$v)
all(near(Z, Z_rec))## [1] TRUE이 때, 행렬 \(\mathbf{V}\)의 각 열벡터가 각 주성분을 도출하는 선형식의 계수가 된다. 즉, 행렬 \(\mathbf{V}\)의 첫 번째 열이 위에서 살펴본 새로운 변수 \(\mathbf{t}_1\)를 도출하는 선형식의 계수이다.
svd_Z$v[, 1]## [1] 0.07608427 -0.39463007 0.56970191 -0.55982770
## [5] -0.44778451특이치는 아래와 같이 추출된다.
svd_Z$d## [1] 6.8516318 5.2245674 3.0593417 1.0435870 0.5571285이 특이치들은 아래 분광분해에서 살펴볼 고유치의 제곱근이다.
3.2.5 분광분해 (Spectral Decomposition)
임의의 정방행렬 \(\mathbf{A}\)에 대하여
\[\mathbf{A}\mathbf{v} = \lambda\mathbf{v} \]
가 성립하는 벡터 \(\mathbf{v} \neq \mathbf{0}\)과 상수 \(\lambda\)가 존재할 때, 상수 \(\lambda\)를 행렬 \(\mathbf{A}\)의 고유치(eigenvalue)라 하며, \(\mathbf{v}\)를 이에 대응하는 고유벡터(eigenvector)라 한다. 통상 \(\mathbf{v}^\top \mathbf{v} = 1\)을 가정한다.
분광분해는 정방행렬을 고유치와 고유벡터의 곱으로 분해하는 방법이다. \((r \times r)\) 정방행렬 \(\mathbf{A}\)에 대해 \(r\)개의 고유치 \(\lambda_1, \cdots, \lambda_r\)와 고유벡터 \(\mathbf{v}_1, \cdots, \mathbf{v}_r\)이 존재한다고 할 때, 행렬 \(\mathbf{A}\)는 다음과 같이 정리된다.
\[ \mathbf{A}\left[\mathbf{v}_1 \, \cdots \, \mathbf{v}_r\right] = \left[\mathbf{v}_1 \, \cdots \, \mathbf{v}_r\right] \left[ \begin{array}{c c c c} \lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & & 0\\ \vdots & & \ddots & 0\\ 0 & 0 & \cdots & \lambda_r \end{array} \right] \\ \mathbf{A} = \mathbf{A} \left[\mathbf{v}_1 \, \cdots \, \mathbf{v}_r\right] \left[\mathbf{v}_1 \, \cdots \, \mathbf{v}_r\right]^{-1} = \left[\mathbf{v}_1 \, \cdots \, \mathbf{v}_r\right] \left[ \begin{array}{c c c c} \lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & & 0\\ \vdots & & \ddots & 0\\ 0 & 0 & \cdots & \lambda_r \end{array} \right] \left[\mathbf{v}_1 \, \cdots \, \mathbf{v}_r\right]^{-1} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^{-1} \]
특히 행렬 \(\mathbf{A}\)가 대칭(symmetric)행렬인 경우, 고유벡터들은 서로 직교하므로 (\(\mathbf{V}\mathbf{V}^\top = \mathbf{I}\)), 위 식을 아래와 같이 표현할 수 있다.
\[ \mathbf{A} = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^\top \]
주성분 분석을 위해 정방행렬 \(\mathbf{Z}^\top \mathbf{Z}\)를 분해를 살펴보자. 식 (3.3)로부터,
\[ \mathbf{Z}^\top \mathbf{Z} = \mathbf{V} \mathbf{D}^\top \mathbf{U}^\top \mathbf{U} \mathbf{D} \mathbf{V}^\top = \mathbf{V} \mathbf{D}^2 \mathbf{V}^\top = \mathbf{V} \mathbf{\Lambda} \mathbf{V}^\top \]
즉, 분광분해를 통해 도출된 고유벡터들의 행렬 \(\mathbf{V}\)의 각 열벡터가 각 주성분을 도출하는 선형식의 계수를 나타내며, 대각행렬 \(\mathbf{\Lambda}\)의 각 대각원소값인 고유치는 특이치의 제곱임을 알 수 있다.
R 함수 eigen을 이용하여 분광분해를 아래와 같이 수행하여 보자.
eig_Z <- eigen(t(Z) %*% Z, symmetric = TRUE)
eig_Z## eigen() decomposition
## $values
## [1] 46.9448582 27.2961041 9.3595718 1.0890737 0.3103922
##
## $vectors
## [,1] [,2] [,3] [,4]
## [1,] -0.07608427 -0.77966993 0.0008915975 -0.140755404
## [2,] 0.39463007 -0.56541218 -0.2953216494 0.117644166
## [3,] -0.56970191 -0.16228156 0.2412221065 -0.637721889
## [4,] 0.55982770 0.19654293 -0.2565972887 -0.748094314
## [5,] 0.44778451 -0.08636803 0.8881182665 -0.003668418
## [,5]
## [1,] 0.60540325
## [2,] -0.65078503
## [3,] -0.42921686
## [4,] 0.14992183
## [5,] -0.05711464결과에서 values는 행렬 \(\mathbf{Z}^\top \mathbf{Z}\)의 고유치(eigenvalue)들이다. 이들이 앞 장의 특이치 분해에서 얻은 특이치들의 제곱임을 확인하여 보자.
all(near(eig_Z$values, svd_Z$d ^ 2))## [1] TRUE또한 분광분해 결과 vectors의 각 열은 행렬 \(\mathbf{Z}^\top \mathbf{Z}\)의 고유벡터(eigenvector)들이다. 이들이 앞 장의 특이치 분해에서 얻은 계수 행렬과 동일함을 확인하여 보자.
all(near(eig_Z$vectors, svd_Z$v))## [1] FALSE이 경우 두 행렬이 동일하지 않게 나타날 수 있는데, 그 이유는 경우에 따라 어떤 주성분을 생성하는 선형계수 부호가 정반대인 형태로 얻어질 수 있기 때문이다. 주성분의 설명력은 선형계수의 부호에 영향을 받지 않는다.
두 행렬의 계수 부호가 서로 동일하게 조정한 뒤 행렬을 비교해보자.
sign_adjust <- 1 - 2 * ((eig_Z$vectors * svd_Z$v) < 0)
all(near(eig_Z$vectors * sign_adjust, svd_Z$v))## [1] TRUE위 각 고유값들을 고유값들의 총합으로 나누면, 각 고유벡터에 해당하는 주성분이 설명하는 총변동의 비율을 얻을 수 있다.
eig_Z$values / sum(eig_Z$values)## [1] 0.552292449 0.321130636 0.110112610 0.012812632
## [5] 0.003651673평균 및 분산 조정된 \(\mathbf{Z}\)의 분산-공분산 행렬은 아래와 같다.
\[\frac{1}{n - 1} \mathbf{Z}^\top \mathbf{Z}\]
all(near(cov(Z), t(Z) %*% Z / (nrow(Z) - 1)))## [1] TRUE여기에 위에서 구한 분광분해를 대입하면,
\[\frac{1}{n - 1} \mathbf{Z}^\top \mathbf{Z} = \frac{1}{n - 1} \mathbf{V} \mathbf{\Lambda} \mathbf{V}^\top = \mathbf{V} \left( \frac{1}{n - 1} \mathbf{\Lambda} \right) \mathbf{V}^\top\]
따라서, \(\mathbf{Z}\)의 분산-공분산 행렬에 대한 분광분해 결과, 고유벡터 행렬 \(\mathbf{V}\)는 앞에서 구한 \(\mathbf{Z}^\top \mathbf{Z}\)의 고유벡터 행렬들과 동일하며, 고유값은 앞에서 구한 \(\mathbf{Z}^\top \mathbf{Z}\)의 고유값을 \((n - 1)\)으로 나눈 값이다.
eig_cov_Z <- eigen(cov(Z))
eig_cov_Z## eigen() decomposition
## $values
## [1] 2.76146225 1.60565318 0.55056305 0.06406316 0.01825836
##
## $vectors
## [,1] [,2] [,3] [,4]
## [1,] -0.07608427 0.77966993 0.0008915975 -0.140755404
## [2,] 0.39463007 0.56541218 -0.2953216494 0.117644166
## [3,] -0.56970191 0.16228156 0.2412221065 -0.637721889
## [4,] 0.55982770 -0.19654293 -0.2565972887 -0.748094314
## [5,] 0.44778451 0.08636803 0.8881182665 -0.003668418
## [,5]
## [1,] 0.60540325
## [2,] -0.65078503
## [3,] -0.42921686
## [4,] 0.14992183
## [5,] -0.05711464all(near(eig_cov_Z$values, eig_Z$values / (nrow(Z) - 1)))## [1] TRUE또한 이 결과는 평균 및 분산조정 이전 원 데이터의 상관행렬(correlation matrix)에 대해 분광분해를 수행한 결과와 동일하다.
eig_cor_raw <- eigen(cor(train_df[, -1]))
eig_cor_raw## eigen() decomposition
## $values
## [1] 2.76146225 1.60565318 0.55056305 0.06406316 0.01825836
##
## $vectors
## [,1] [,2] [,3] [,4]
## [1,] -0.07608427 0.77966993 0.0008915975 -0.140755404
## [2,] 0.39463007 0.56541218 -0.2953216494 0.117644166
## [3,] -0.56970191 0.16228156 0.2412221065 -0.637721889
## [4,] 0.55982770 -0.19654293 -0.2565972887 -0.748094314
## [5,] 0.44778451 0.08636803 0.8881182665 -0.003668418
## [,5]
## [1,] 0.60540325
## [2,] -0.65078503
## [3,] -0.42921686
## [4,] 0.14992183
## [5,] -0.05711464all(near(eig_cov_Z$values, eig_cor_raw$values))## [1] TRUEall(near(eig_cov_Z$vectors, eig_cor_raw$vectors))## [1] TRUE3.2.6 NIPALS 알고리즘
NIPALS(Nonlinear Iterative Paritial Least Squares) 알고리즘은 반복적(iterative) 알고리즘을 이용하여 변동 기여율이 가장 큰 주성분부터 가장 작은 주성분까지 순차적으로 고유벡터와 주성분 스코어를 구하는 방법이다.
우선, 특이치 분해에서 사용한 식을 단순화하여, 분산조정된 행렬 \(\mathbf{Z}\)가 아래와 같이 주성분 스코어 행렬 \(\mathbf{T}\)와 고유벡터 행렬 \(\mathbf{V}\)로 분해된다고 하자. (분산조정 대신 평균조정만을 원할 경우 \(\mathbf{Z}\) 대신 \(\mathbf{X}\)를 사용)
\[ \mathbf{Z} = \mathbf{U} \mathbf{D} \mathbf{V}^\top = \mathbf{T} \mathbf{V}^\top \]
즉, 주성분 스코어 \(\mathbf{T}\)는 아래와 같다.
\[ \mathbf{T} = \mathbf{Z} \mathbf{V} \]
T_mat <- Z %*% svd_Z$v
T_mat## [,1] [,2] [,3] [,4]
## [1,] -1.4870243 0.6066594 -0.63361774 -0.29625002
## [2,] -0.2063797 -0.0804627 -0.04965017 0.26323513
## [3,] 0.1968538 0.9704605 -0.39507856 0.27123746
## [4,] -2.3542884 -3.5056480 0.16252734 0.02524924
## [5,] -0.8953707 1.4552899 1.36265905 0.20161775
## [6,] -0.3682082 -0.5976313 0.65857722 0.27901317
## [7,] -0.9354306 -1.4144519 -0.82574638 0.07358977
## [8,] 2.4129728 -0.6785064 0.92207607 -0.36161577
## [9,] 2.6991862 -0.7596591 -0.45091077 -0.21030378
## [10,] -0.4050098 0.2800099 -0.92835441 0.13993488
## [11,] 1.3958199 1.1353513 -0.09819177 0.34335126
## [12,] -1.5381192 1.1576616 -0.07467334 -0.29404424
## [13,] 0.3217681 -0.2378023 1.10180230 0.28507243
## [14,] -2.0306806 0.9646122 0.20906175 -0.39639758
## [15,] 3.0389460 0.8841645 -0.77478769 -0.04079854
## [16,] 2.0064063 -1.2831337 0.64388897 -0.22077705
## [17,] -0.4211779 -0.2987099 -1.20644766 0.11766274
## [18,] -1.4302634 1.4017959 0.37686579 -0.17977686
## [,5]
## [1,] 0.020293731
## [2,] 0.063581473
## [3,] 0.103351746
## [4,] -0.249920974
## [5,] -0.055517167
## [6,] 0.060458248
## [7,] 0.095960908
## [8,] -0.062593521
## [9,] 0.168645128
## [10,] 0.001811118
## [11,] -0.094986796
## [12,] 0.052430946
## [13,] 0.030666763
## [14,] -0.085778570
## [15,] -0.349688462
## [16,] 0.188366871
## [17,] 0.068250991
## [18,] 0.044667568NIPALS 알고리즘은 아래와 같이 주성분 스코어 행렬 \(\mathbf{T}\)의 열과 고유벡터행렬 \(\mathbf{V}\)의 열을 동시에 구한다.
- [단계 0] 반복알고리즘 수행을 위한 초기화를 한다. \(h \leftarrow 1\), \(\mathbf{Z}_h \leftarrow \mathbf{Z}\).
- [단계 1] 데이터 행렬 \(\mathbf{Z}_h\)의 임의의 열 하나를 주성분 스코어 벡터 \(\mathbf{t}_h\)로 선정한다.
- [단계 2] 로딩벡터를 구한다. \(\mathbf{v}_h \leftarrow \mathbf{Z}_h \mathbf{t}_h \left/ \sqrt{\mathbf{t}_h^\top \mathbf{t}_h} \right.\)
- [단계 3] 로딩벡터의 크기가 1이 되도록 한다. \(\mathbf{v}_h \leftarrow \mathbf{v}_h \left/ \sqrt{\mathbf{v}_h^\top \mathbf{v}_h} \right.\)
- [단계 4] 주성분 스코어 벡터를 로딩벡터에 기반하여 계산한다. \(\mathbf{t}_h \leftarrow \mathbf{Z}_h \mathbf{v}_h\)
- [단계 5] 주성분 스코어 벡터 \(\mathbf{t}_h\)가 수렴하였으면 [단계 6]으로 진행하고, 그렇지 않으면 [단계 2]로 돌아간다.
- [단계 6] 데이터 행렬 \(\mathbf{Z}_h\)로부터 새로 얻어진 주성분 벡터 \(\mathbf{t}_h\)와 고유벡터 \(\mathbf{v}_h\)가 설명하는 부분을 제거하고 나머지 변동만을 담은 새로운 데이터 행렬 \(\mathbf{Z}_{h + 1}\)을 구한다. \[ \mathbf{Z}_{h + 1} \leftarrow \mathbf{Z}_{h} - \mathbf{t}_h \mathbf{v}_h^\top \]
- [단계 7] \(h \leftarrow h + 1\)로 업데이트하고, [단계 1]로 돌아간다. [단계 1] - [단계 7]의 과정을 \(\mathbf{Z}\)의 rank 수만큼의 주성분을 얻을 때까지 반복한다.
위 반복 알고리즘을 수행하는 함수를 아래와 같이 구성해보자. 아래 함수에서 입력변수 X는 데이터 행렬으로, 평균조정된 행렬 \(\mathbf{X}\)나 분산조정된 \(\mathbf{Z}\) 모두 사용 가능하다. 입력변수 r은 추출하고자 하는 주성분의 개수이다.
nipals_pca <- function(X, r = NULL) {
if (is_empty(r) || (r > min(dim(X)))) {
r <- min(dim(X))
}
Th <- matrix(NA, nrow = nrow(X), ncol = r)
Vh <- matrix(NA, nrow = ncol(X), ncol = r)
for (h in seq_len(r)) {
# 단계 1
j <- sample(ncol(X), 1)
Th[, h] <- X[, j]
while (TRUE) {
# 단계 2
Vh[, h] <- t(t(Th[, h]) %*% X / (norm(Th[, h], "2") ^ 2))
# 단계 3
Vh[, h] <- Vh[, h] / norm(Vh[, h], "2")
# 단계 4
th <- X %*% Vh[, h]
# 단계 5
if (all(near(Th[, h], th))) break
Th[, h] <- th
}
#단계 6
X <- X - Th[, h] %*% t(Vh[, h])
}
return(list(T = Th, V = Vh))
}
nipals_Z <- nipals_pca(Z)
nipals_Z## $T
## [,1] [,2] [,3] [,4]
## [1,] 1.4870243 -0.6066594 0.63361773 0.29625002
## [2,] 0.2063797 0.0804627 0.04965018 -0.26323513
## [3,] -0.1968538 -0.9704605 0.39507856 -0.27123746
## [4,] 2.3542884 3.5056480 -0.16252732 -0.02524925
## [5,] 0.8953707 -1.4552899 -1.36265906 -0.20161776
## [6,] 0.3682082 0.5976313 -0.65857721 -0.27901317
## [7,] 0.9354306 1.4144519 0.82574638 -0.07358976
## [8,] -2.4129728 0.6785064 -0.92207607 0.36161576
## [9,] -2.6991862 0.7596591 0.45091077 0.21030379
## [10,] 0.4050098 -0.2800099 0.92835441 -0.13993488
## [11,] -1.3958199 -1.1353513 0.09819177 -0.34335127
## [12,] 1.5381192 -1.1576616 0.07467333 0.29404424
## [13,] -0.3217681 0.2378023 -1.10180229 -0.28507243
## [14,] 2.0306806 -0.9646122 -0.20906177 0.39639757
## [15,] -3.0389460 -0.8841645 0.77478769 0.04079852
## [16,] -2.0064063 1.2831337 -0.64388896 0.22077706
## [17,] 0.4211779 0.2987099 1.20644767 -0.11766274
## [18,] 1.4302634 -1.4017959 -0.37686580 0.17977686
## [,5]
## [1,] -0.02029373
## [2,] -0.06358148
## [3,] -0.10335175
## [4,] 0.24992097
## [5,] 0.05551716
## [6,] -0.06045825
## [7,] -0.09596091
## [8,] 0.06259353
## [9,] -0.16864512
## [10,] -0.00181112
## [11,] 0.09498679
## [12,] -0.05243094
## [13,] -0.03066677
## [14,] 0.08577858
## [15,] 0.34968846
## [16,] -0.18836687
## [17,] -0.06825099
## [18,] -0.04466756
##
## $V
## [,1] [,2] [,3] [,4]
## [1,] -0.07608427 0.77966993 -0.0008915859 0.140755413
## [2,] 0.39463007 0.56541218 0.2953216581 -0.117644173
## [3,] -0.56970191 0.16228156 -0.2412221050 0.637721878
## [4,] 0.55982770 -0.19654293 0.2565972845 0.748094320
## [5,] 0.44778451 0.08636803 -0.8881182652 0.003668405
## [,5]
## [1,] -0.60540325
## [2,] 0.65078502
## [3,] 0.42921690
## [4,] -0.14992178
## [5,] 0.05711464위 분해된 행렬의 곱이 원 데이터 행렬 \(\mathbf{Z}\)과 일치하는지 확인해보자.
all(near(Z, nipals_Z$T %*% t(nipals_Z$V)))## [1] TRUER 패키지 nipals내의 함수 nipals가 이 장에서 설명한 NIPALS 알고리즘에 기반한 주성분 분석을 아래와 같이 제공한다.
library(nipals)
nipals(Z, center = FALSE, scale = FALSE)## $eig
## [1] 6.8516317 5.2245674 3.0593417 1.0435869 0.5571285
##
## $scores
## PC1 PC2 PC3 PC4
## [1,] -0.21705404 -0.11608067 -0.20710543 0.28388475
## [2,] -0.03011834 0.01540551 -0.01623006 -0.25221776
## [3,] 0.02869590 -0.18575892 -0.12913406 -0.25987079
## [4,] -0.34348333 0.67105909 0.05310696 -0.02428657
## [5,] -0.13073246 -0.27851123 0.44541637 -0.19321728
## [6,] -0.05371865 0.11440401 0.21526389 -0.26733867
## [7,] -0.13647563 0.27074924 -0.26991736 -0.07048155
## [8,] 0.35219939 0.12981093 0.30139420 0.34648877
## [9,] 0.39397535 0.14532356 -0.14739177 0.20158102
## [10,] -0.05912155 -0.05359220 -0.30344792 -0.13408884
## [11,] 0.20367981 -0.21735017 -0.03209051 -0.32904441
## [12,] -0.22453126 -0.22153804 -0.02440174 0.28178254
## [13,] 0.04697085 0.04551641 0.36014173 -0.27315578
## [14,] -0.29641393 -0.18457147 0.06834143 0.37981073
## [15,] 0.44350417 -0.16932257 -0.25324815 0.03896920
## [16,] 0.29288258 0.24554714 0.21046020 0.21162296
## [17,] -0.06146040 0.05717479 -0.39435062 -0.11272299
## [18,] -0.20879845 -0.26826541 0.12319285 0.17228468
## PC5
## [1,] -0.036368396
## [2,] -0.114174269
## [3,] -0.185560165
## [4,] 0.448582844
## [5,] 0.099609669
## [6,] -0.108571464
## [7,] -0.172255999
## [8,] 0.112419837
## [9,] -0.302663550
## [10,] -0.003277662
## [11,] 0.170427304
## [12,] -0.094052577
## [13,] -0.055099430
## [14,] 0.154041866
## [15,] 0.627670066
## [16,] -0.338060584
## [17,] -0.122527440
## [18,] -0.080140048
##
## $loadings
## PC1 PC2 PC3
## roa 0.07627711 0.7796534 0.0008551484
## roe -0.39449021 0.5654941 -0.2953469599
## bis 0.56974203 0.1621586 0.2412197864
## de_ratio -0.55987629 -0.1964075 -0.2565837179
## turnover -0.44776314 0.0865197 0.8881144365
## PC4 PC5
## roa 0.140974596 -0.60534928
## roe -0.117893972 0.65074198
## bis 0.637556663 0.42945678
## de_ratio 0.748154680 -0.14963952
## turnover 0.003640124 0.05711403
##
## $fitted
## NULL
##
## $ncomp
## [1] 5
##
## $R2
## [1] 0.552292435 0.321130644 0.110112610 0.012812631
## [5] 0.003651673
##
## $iter
## [1] 14 4 4 6 3
##
## $center
## [1] NA
##
## $scale
## [1] NA평균 및 분산조정 이전의 원래 데이터를 입력하고, 파라미터 center(평균조정) 및 scale(분산조정)의 값을 모두 TRUE로 설정하면 동일한 결과를 얻을 수 있다.
library(nipals)
nipals(train_df[, -1], center = TRUE, scale = TRUE)## $eig
## [1] 6.8516317 5.2245674 3.0593417 1.0435869 0.5571285
##
## $scores
## PC1 PC2 PC3 PC4
## [1,] -0.21705404 -0.11608067 -0.20710543 0.28388475
## [2,] -0.03011834 0.01540551 -0.01623006 -0.25221776
## [3,] 0.02869590 -0.18575892 -0.12913406 -0.25987079
## [4,] -0.34348333 0.67105909 0.05310696 -0.02428657
## [5,] -0.13073246 -0.27851123 0.44541637 -0.19321728
## [6,] -0.05371865 0.11440401 0.21526389 -0.26733867
## [7,] -0.13647563 0.27074924 -0.26991736 -0.07048155
## [8,] 0.35219939 0.12981093 0.30139420 0.34648877
## [9,] 0.39397535 0.14532356 -0.14739177 0.20158102
## [10,] -0.05912155 -0.05359220 -0.30344792 -0.13408884
## [11,] 0.20367981 -0.21735017 -0.03209051 -0.32904441
## [12,] -0.22453126 -0.22153804 -0.02440174 0.28178254
## [13,] 0.04697085 0.04551641 0.36014173 -0.27315578
## [14,] -0.29641393 -0.18457147 0.06834143 0.37981073
## [15,] 0.44350417 -0.16932257 -0.25324815 0.03896920
## [16,] 0.29288258 0.24554714 0.21046020 0.21162296
## [17,] -0.06146040 0.05717479 -0.39435062 -0.11272299
## [18,] -0.20879845 -0.26826541 0.12319285 0.17228468
## PC5
## [1,] -0.036368396
## [2,] -0.114174269
## [3,] -0.185560165
## [4,] 0.448582844
## [5,] 0.099609669
## [6,] -0.108571464
## [7,] -0.172255999
## [8,] 0.112419837
## [9,] -0.302663550
## [10,] -0.003277662
## [11,] 0.170427304
## [12,] -0.094052577
## [13,] -0.055099430
## [14,] 0.154041866
## [15,] 0.627670066
## [16,] -0.338060584
## [17,] -0.122527440
## [18,] -0.080140048
##
## $loadings
## PC1 PC2 PC3
## roa 0.07627711 0.7796534 0.0008551484
## roe -0.39449021 0.5654941 -0.2953469599
## bis 0.56974203 0.1621586 0.2412197864
## de_ratio -0.55987629 -0.1964075 -0.2565837179
## turnover -0.44776314 0.0865197 0.8881144365
## PC4 PC5
## roa 0.140974596 -0.60534928
## roe -0.117893972 0.65074198
## bis 0.637556663 0.42945678
## de_ratio 0.748154680 -0.14963952
## turnover 0.003640124 0.05711403
##
## $fitted
## NULL
##
## $ncomp
## [1] 5
##
## $R2
## [1] 0.552292435 0.321130644 0.110112610 0.012812631
## [5] 0.003651673
##
## $iter
## [1] 14 4 4 6 3
##
## $center
## roa roe bis de_ratio
## 3.0350000 9.3505556 35.1116667 250.1477778
## turnover
## 0.8816667
##
## $scale
## roa roe bis de_ratio
## 1.1356949 4.5692430 18.1343662 143.0378269
## turnover
## 0.36181323.3 주성분 회귀분석
2.2 장에서 살펴본 다중회귀모형의 식 (2.2)을 아래에 다시 살펴보자.
\[\begin{equation} \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\epsilon} \tag{3.4} \end{equation}\]
여기서, \(\boldsymbol{\beta}\) 와 \(\boldsymbol{\epsilon}\)는 각각 회귀계수와 오차항을 나타내는 벡터이며, 독립변수 데이터 행렬 \(\mathbf{X}\)와 종속변수 관측치 벡터 \(\mathbf{y}\) 모두 평균조정한 데이터라 간주하자. \(\mathbf{X}\)의 열벡터 간 다중공선성(multicollinearity)이 높으면 최소자승법에 의한 \(\boldsymbol{\beta}\)의 추정치의 분산이 커지는 문제가 있으며, \(\mathbf{X}\) 행렬의 관측수보다 변수 수가 많을 때는 \(\boldsymbol{\beta}\) 추정치를 구할 수 없다. 이 문제를 해결하기 위해 주성분 회귀분석(principal component regression; PCR)에서는 \(\mathbf{X}\) 변동 대부분을 설명하는 \(A\)개 (\(A \leq rank(\mathbf{X})\))의 주성분 스코어를 다음과 같이 독립변수로 사용한다.
\[\begin{equation} \mathbf{y} = q_1 \mathbf{t}_1 + q_2 \mathbf{t}_2 + \cdots + q_A \mathbf{t}_A + \mathbf{f} \tag{3.5} \end{equation}\]
여기서 \(\mathbf{f}\)는 오차항을 나타내는 벡터이며, \(q_1, \cdots, q_A\)는 회귀계수들이다. 이 때, \(A\)개의 주성분 스코어로 구성되는 \((n \times A)\) 주성분행렬을 \(\mathbf{T}_A = [\mathbf{t}_1 \, \cdots \, \mathbf{t}_A]\)로, 회귀계수벡터를 \(\mathbf{q} = [q_1 \, \cdots \, q_A]^\top\)으로 표기하면, 식 (3.5)의 모형은 다음과 같이 표현된다.
\[\begin{equation} \mathbf{y} = \mathbf{T}_A \mathbf{q}_A + \mathbf{f} \tag{3.6} \end{equation}\]
위 모형은 다중회귀모형으로 볼 수 있으므로, 다중회귀모형에 대한 모든 이론이 적용될 수 있다. 또한 위 모형에서 각 주성분 스코어 벡터 \(\mathbf{t}_1, \cdots, \mathbf{t}_A\)는 서로 선형 독립적(linearly independent)이므로, 회귀성 검정이 용이한 측면이 있다.
3.3.1 기본 R 스트립트
3개의 독립변수와 1개의 종속변수(y)를 관측한 데이터가 아래와 같다고 하자.
train_df <- tribble(
~x1, ~x2, ~x3, ~y,
-3, -3, 5, -30,
-2, -3, 7, -20,
0, 0, 4, 0,
1, 2, 0, 5,
2, 2, -5, 10,
2, 2, -11, 35
)
knitr::kable(
train_df, booktabs = TRUE,
align = rep("r", ncol(train_df)),
caption = "주성분 회귀분석 예제 데이터"
)| x1 | x2 | x3 | y |
|---|---|---|---|
| -3 | -3 | 5 | -30 |
| -2 | -3 | 7 | -20 |
| 0 | 0 | 4 | 0 |
| 1 | 2 | 0 | 5 |
| 2 | 2 | -5 | 10 |
| 2 | 2 | -11 | 35 |
3개의 독립변수로 이루어진 데이터에서 2개의 주성분만을 추출하여 회귀모형을 추정하여 보자.
pcr_fit <- pls::pcr(y ~ x1 + x2 + x3, data = train_df, ncomp = 2)
coef(pcr_fit, intercept = TRUE)## , , 2 comps
##
## y
## (Intercept) 0.000000
## x1 2.130440
## x2 2.721789
## x3 -1.737825위 회귀계수들은 주성분을 이용하여 추정한 회귀 모형을 원래 독립변수를 이용한 회귀식(평균조정 이전)으로 다시 선형변환한 결과이다. 이에 대해서는 다음 절에서 좀 더 자세히 살펴보도록 하자.
summary(pcr_fit)## Data: X dimension: 6 3
## Y dimension: 6 1
## Fit method: svdpc
## Number of components considered: 2
## TRAINING: % variance explained
## 1 comps 2 comps
## X 94.98 99.79
## y 87.94 91.31위 요약표는 하나의 주성분과 두 개의 주성분을 이용하였을 때 추정된 회귀모형들이 종속변수의 총 변량을 각각 87.9415591%와 91.3101613% 만큼을 설명함을 알려준다.
3.3.2 주성분 회귀계수 추정
우선 Table 3.2의 세 독립변수에 대해 주성분 분석을 수행하여 두 개의 주성분을 추출하자.
pca_fit <- prcomp(train_df[, c("x1", "x2", "x3")], rank. = 2,
center = TRUE, scale. = FALSE)
pca_fit$x## PC1 PC2
## [1,] -6.2346992 1.9880169
## [2,] -7.8320036 0.6817026
## [3,] -3.6996775 -1.5151642
## [4,] 0.8208672 -2.0392493
## [5,] 5.6979984 -0.6940262
## [6,] 11.2475146 1.5787202또한 평균조정된 종속변수 벡터를 계산하자.
y_centered <- train_df$y - mean(train_df$y)
y_centered## [1] -30 -20 0 5 10 35주성분 스코어와 평균조정된 종속변수를 이용하여 회귀모형을 추정하자. 이 때, intercept가 없는 모형을 가정한다.
pc_lm_fit <- lm(y_centered ~ - 1 + pca_fit$x)
coef(pc_lm_fit)## pca_fit$xPC1 pca_fit$xPC2
## 2.918798 -2.539206위 회귀계수 벡터가 식 (3.6)의 회귀계수 벡터 \(\mathbf{q}_A\)의 값이다 (\(A = 2\)).
3.3.3 회귀계수 선형변환
앞장에서 얻어진 주성분을 이용한 회귀식을 원 데이터에서 관측된 독립변수와 종속변수에 대한 식으로 변환하여 보자.
각 주성분은 평균조정된 독립변수들의 선형조합으로 아래와 같이 얻어진다.
pca_fit$rotation## PC1 PC2
## x1 0.2525343 -0.5487321
## x2 0.2841664 -0.7452586
## x3 -0.9249194 -0.3787911따라서, 아래와 같이 주성분에 대한 회귀계수를 원래 독립변수(평균조정 이후)에 대한 회귀계수로 변환할 수 있다.
beta_x <- pca_fit$rotation %*% coef(pc_lm_fit)
beta_x## [,1]
## x1 2.130440
## x2 2.721789
## x3 -1.737825Intercept는 평균조정 이전 종속변수의 평균에서 위 회귀계수벡터를 평균조정 이전 독립변수의 평균벡터와 곱한 결과를 뺀 값이다.
mean(train_df$y) - colMeans(train_df[, c("x1", "x2", "x3")]) %*% beta_x## [,1]
## [1,] 0본 장에서 사용한 Table 3.2는 이미 평균조정이 되어 있어서 Intercept가 0으로 추정된다.
본 장에서 분산조정된 주성분에 대한 회귀계수 변환은 다루지 않았으나, 이 또한 간단하게 변환할 수 있다.