Chapter 13 비계층적 군집방법

비계층적 군집방법(Nonhierarchical clustering)은 분할방법(Partitioning method)이라고도 하는데, 군집의 수 \(K\)를 사전에 지정하고 대상 객체들을 적절한 군집에 배정하는 방법이다. 즉, 이 방법은 \(n\)개의 객체를 \(K\)개의 군집에 할당하는 최적화 문제로 간주할 수 있다. 본 장에서는 분할방법의 대표적인 K-means 알고리즘, K-medoids 군집방법, 퍼지 K-means 알고리즘, 그리고 모형기반 군집방법에 대하여 주로 알아본다.

13.1 필요 R package 설치

본 장에서 필요한 R 패키지들은 아래와 같다.

package	version
tidyverse	1.3.1
stats	4.1.3
cluster	2.1.2
flexclust	1.4-0
mclust	5.4.7
mvtnorm	1.1-2

13.2 K-means 알고리즘

K-means 알고리즘은 비계층적 군집방법 중 가장 널리 사용되는 것으로 \(K\)개 군집의 중심좌표를 고려하여 각 객체를 가까운 군집에 배정하는 반복적 알고리즘이다.

13.2.1 기본 R 스크립트

10명에 대한 PC의 사용경력(\(x_1\))과 주당 사용시간(\(x_2\))이 다음과 같다.

df <- tribble(
  ~id, ~x1, ~x2,
  1, 6, 14,
  2, 8, 13,
  3, 14, 6,
  4, 11, 8,
  5, 15, 7,
  6, 7, 15,
  7, 13, 6,
  8, 5, 4,
  9, 3, 3,
  10, 3, 2
)

df %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r'),
    col.names = c(
      '객체번호', 
      '사용경력($x_1$)', '사용시간($x_2$)'
      ),
    caption = 'PC 사용 데이터'
  )

Table 13.1: PC 사용 데이터

객체번호	사용경력(\(x_1\))	사용시간(\(x_2\))
1	6	14
2	8	13
3	14	6
4	11	8
5	15	7
6	7	15
7	13	6
8	5	4
9	3	3
10	3	2

아래와 같이 stats 패키지의 kmeans 함수를 이용하여 K-means 알고리즘 수행 결과를 얻을 수 있다. 아래 스크립트는 군집 수가 \(K = 3\)라 가정하여 수행한 예이다.

set.seed(123)
kmeans_solution <- kmeans(x = df[, -1], centers = 3)

위 스크립트 실행 결과 도출된 군집 중심좌표는 위에서 얻어진 kmeans 클래스 객체의 centers값에 저장된다.

kmeans_solution$centers

##          x1    x2
## 1 13.250000  6.75
## 2  3.666667  3.00
## 3  7.000000 14.00

또한 각 학습 데이터가 속한 군집은 cluster값에 저장된다.

kmeans_solution$cluster

##  [1] 3 3 1 1 1 3 1 2 2 2

객체의 군집결과는 아래와 같이 도식화하여 보일 수 있다.

df %>%
  mutate(cluster = as.factor(kmeans_solution$cluster)) %>%
  ggplot(aes(x = x1, y = x2)) +
  geom_text(aes(label = id, color = cluster))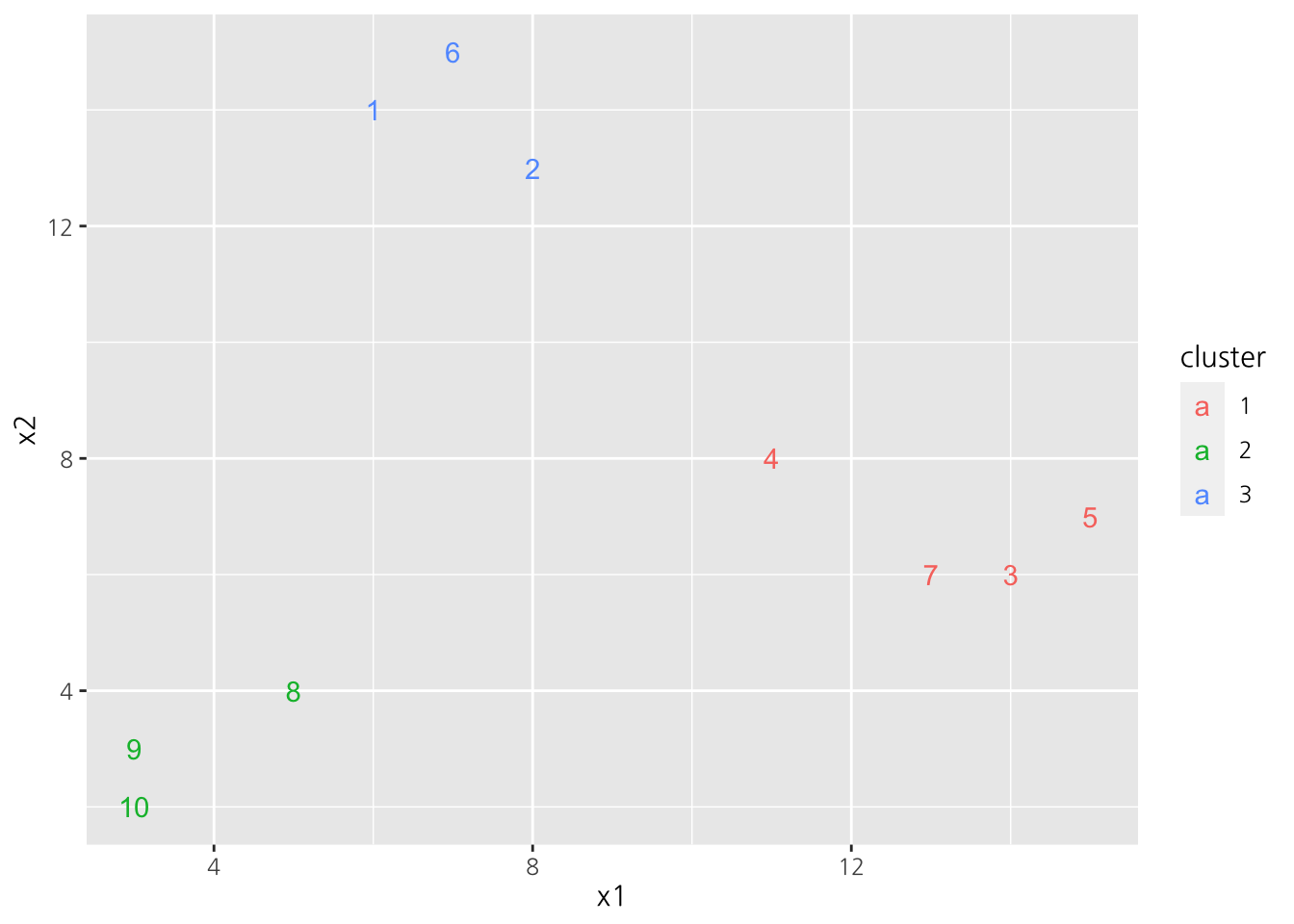

Figure 13.1: K-means 수행 결과

13.2.2 알고리즘

K-means 알고리즘의 구체적 절차는 아래와 같다. Table 13.1에 대한 각 단계의 결과를 함께 살펴보자.

[단계 0] (초기 객체 선정) 어떤 규칙에 의하여 \(K\)개의 객체의 좌표를 초기 군집의 중심좌표(centroid)로 선정한다. 군집 \(j\)의 중심좌표를 \(\mathbf{c}_j = \left(\bar{x}^{(j)}_1, \cdots, \bar{x}^{(j)}_p\right)^\top\)라 하자. 초기 군집 중심좌표 \(\mathbf{c}_1, \cdots, \mathbf{c}_K\)를 선정하는 방법은 예를 들어 다음과 같은 규칙이 사용된다.

• 무작위 방법: 대상 객체 중 무작위로 \(K\)개를 선정한다.
• 외각 객체 선정: 전체 객체의 중심좌표에서 가장 멀리 위치하는 \(K\)개의 객체를 선정한다.

[단계 0] 무작위 방법을 이용하여 Table 13.1으로부터 3개의 객체를 초기 군집 중심좌표로 선정하자.

set.seed(123)

init_cluster <- function(df, k = 1) {
  k <- min(k, nrow(df))
  
  df %>%
    sample_n(k)
}

cluster_df <- init_cluster(df[, -1], 3)

cluster_df

## # A tibble: 3 x 2
##      x1    x2
##   <dbl> <dbl>
## 1    14     6
## 2     3     2
## 3     8    13

[단계 1] (객체의 군집 배정) 각 객체에 대하여 \(K\)개의 군집 중심좌표(centroid)와의 거리(주로 유클리드 거리 사용)를 산출한 후 가장 가까운 군집에 그 객체를 배정한다.

\[\begin{equation*} a_{ij} = \begin{cases} 1 & \text{if } j = \arg\,\max_k d(\mathbf{x}_i, \mathbf{c}_k)\\ 0 & \text{otherwise} \end{cases}, \, i = 1, \cdots, n, \, j = 1, \cdots, K \end{equation*}\]

각 객체에 대하여 3개의 군집 중심좌표와의 거리를 산출해보면 아래와 같다.

flexclust::dist2(df[, -1], cluster_df)

##            [,1]      [,2]      [,3]
##  [1,] 11.313708 12.369317  2.236068
##  [2,]  9.219544 12.083046  0.000000
##  [3,]  0.000000 11.704700  9.219544
##  [4,]  3.605551 10.000000  5.830952
##  [5,]  1.414214 13.000000  9.219544
##  [6,] 11.401754 13.601471  2.236068
##  [7,]  1.000000 10.770330  8.602325
##  [8,]  9.219544  2.828427  9.486833
##  [9,] 11.401754  1.000000 11.180340
## [10,] 11.704700  0.000000 12.083046

이에 각 객체들에 대해 거리가 가장 가까운 군집에 그 객체를 배정한다.

assign_cluster <- function(df, cluster_df) {
  cluster_ind <- flexclust::dist2(df, cluster_df) %>%
    apply(1, which.min)
  
  map(unique(cluster_ind), ~which(cluster_ind == .))
}

cluster_objects <- assign_cluster(df[, -1], cluster_df)

cluster_objects

## [[1]]
## [1] 1 2 6
## 
## [[2]]
## [1] 3 4 5 7
## 
## [[3]]
## [1]  8  9 10

[단계 2] (군집 중심좌표의 산출) 새로운 군집에 대한 중심좌표를 산출한다.

\[\begin{equation*} \bar{x}^{(j)}_l = \frac{\sum_{i} a_{ij} x_{li}}{\sum_{i} a_{ij}}, \, l = 1, \cdots, p, \, j = 1, \cdots, K \end{equation*}\]

find_center <- function(df, cluster) {
  map_dfr(cluster, ~df[., ] %>% summarize_all(mean)) 
}

new_cluster_df <- find_center(df[, -1], cluster_objects)

new_cluster_df

## # A tibble: 3 x 2
##      x1    x2
##   <dbl> <dbl>
## 1  7    14   
## 2 13.2   6.75
## 3  3.67  3

[단계 3] (수렴 조건 점검) 새로 산출된 중심좌표값과 이전 좌표값을 비교하여 수렴 조건 내에 들면 마치며, 그렇지 않으면 단계 1을 반복한다.

identical(cluster_df, new_cluster_df)

## [1] FALSE

위의 경우, 군집 중심좌표가 다르므로 다음 iteration을 진행한다.

13.2.3 R 스크립트 구현

위의 과정을 군집해가 수렴할 때까지 반복하도록 아래와 같이 R 스크립트를 구현해보자.

init_cluster <- function(df, k = 1) {
  k <- min(k, nrow(df))
  
  df %>% sample_n(k)
}

assign_cluster <- function(df, cluster_df) {
  cluster_ind <- flexclust::dist2(df, cluster_df) %>%
    apply(1, which.min)
  
  map(unique(cluster_ind), ~which(cluster_ind == .))
}

find_center <- function(df, cluster) {
  map_dfr(cluster, ~df[., ] %>% summarize_all(mean)) 
}

kmeans_cluster <- function(df, k = 1, verbose = FALSE) {
  k <- min(k, nrow(df))
  
  i <- 0L
  
  ## 단계 0
  cluster_df <- init_cluster(df, k)
  
  while(TRUE) {
    i <- i + 1L
    
    ## 단계 1
    cluster_objects <- assign_cluster(df, cluster_df)
    if (verbose) { # 군집해 출력
      cat("Iteration", i, ":", 
          map(cluster_objects, ~ str_c("{", str_c(., collapse = ", "), "}")) %>%
            str_c(collapse = ", "),
          "\n"
      )
    }
    
    ## 단계 2
    new_cluster_df <- find_center(df, cluster_objects)

    ## 단계 3
    if(identical(cluster_df, new_cluster_df)) break
    
    cluster_df <- new_cluster_df
  }
  
  res <- list(
    cluster_centers = cluster_df,
    assgined_objects = cluster_objects,
    n_iteration = i
  )
  
  return (res)
}

set.seed(123)

kmeans_solution <- kmeans_cluster(df[, -1], k = 3, verbose = TRUE)

## Iteration 1 : {1, 2, 6}, {3, 4, 5, 7}, {8, 9, 10} 
## Iteration 2 : {1, 2, 6}, {3, 4, 5, 7}, {8, 9, 10}

위와 같이 2번째 Iteration에서 군집해가 수렴하였으며, 최종 군집해는 아래와 같다.

kmeans_solution$assgined_objects

## [[1]]
## [1] 1 2 6
## 
## [[2]]
## [1] 3 4 5 7
## 
## [[3]]
## [1]  8  9 10

13.3 K-medoids 군집방법

K-means 알고리즘에서는 각 군집의 중심좌표(centroid)를 군집 중심으로 고려하고 있는 반면, K-medoids 군집방법에서는 각 군집의 대표객체를 군집 중심으로 고려한다.

K-medoids 군집방법의 알고리즘으로 잘 알려진 것에는 다음과 같은 것들이 있다.

1. PAM(Partitioning Around Medoids)
2. CLARA(Clustering LARge Applications)
3. CLARANS(Clustering Large Applications based on RANdomized Search)
4. K-means-like 알고리즘

13.3.1 PAM 알고리즘

PAM 알고리즘은 Kaufman and Rousseeuw (1990) 에 의하여 발표된 것으로, 초기 대표객체를 선정하는 방법인 BUILD와 더 나은 군집해를 찾아나가는 과정인 SWAP의 두 부분으로 구성되어 있다.

13.3.1.1 기본 R 스크립트

df <- tribble(
  ~id, ~x1, ~x2,
  1, 3, 3,
  2, 5, 4,
  3, 11, 8,
  4, 13, 6,
  5, 14, 6,
  6, 15, 7
)

df %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r'),
    col.names = c(
      '객체번호', 
      '사용경력($x_1$)', '사용시간($x_2$)'
      ),
    caption = 'PC 사용자 데이터'
  )

Table 13.2: PC 사용자 데이터

객체번호	사용경력(\(x_1\))	사용시간(\(x_2\))
1	3	3
2	5	4
3	11	8
4	13	6
5	14	6
6	15	7

PAM 알고리즘은 cluster 패키지 내의 함수 pam을 이용하여 아래와 같이 간단하게 실행할 수 있다.

pam_solution <- cluster::pam(df[, -1], k = 2)

얻어진 pam 객체의 원소 id.med는 몇 번째 객체가 군집의 대표객체로 선정되었는지를 나타낸다.

pam_solution$id.med

## [1] 2 5

또한 pam 객체의 원소 clustering은 각 객체가 어떠한 군집에 할당되었는지를 보여준다.

pam_solution$clustering

## [1] 1 1 2 2 2 2

13.3.1.2 PAM 알고리즘

PAM 알고리즘의 각 단계를 Table 13.2의 예제 데이터에 적용하여 살펴보기로 하자.

13.3.1.2.1 BUILD

BUILD는 다음 절차들을 거쳐서 \(K\)개의 초기 대표객체를 구하는 과정이다.

[단계 0] 우선 각 객체별로 다른 객체 간의 거리를 구한 후, 그 합이 가장 작은 객체 하나를 대표객체로 선정한다. 선정된 대표객체집합을 \(M\)이라 하자.

pairwise_distance_df <- dist(df[, -1], upper = TRUE) %>%
  broom::tidy() %>%
  mutate_if(is.factor, ~ as.integer(as.character(.)))

M_idx <- pairwise_distance_df %>%
  group_by(item1) %>%
  summarize(sum_distance = sum(distance)) %>%
  top_n(-1, sum_distance) %>%
  .$item1

M <- df[M_idx, ]

M

## # A tibble: 1 x 3
##      id    x1    x2
##   <dbl> <dbl> <dbl>
## 1     4    13     6

[단계 1] 대표객체로 선정되지 않은 객체 \(j\)에 대하여, 이전에 대표객체로 선정된 객체들 중 객체 \(j\)에 가장 가까운 거리 \(D_j\)를 구한다. 즉,

\[\begin{equation*} D_j = \min_{k \in M} d(j, k), \, j \notin M \end{equation*}\]

D_j <- pairwise_distance_df %>%
  filter(
    !item1 %in% M$id,
    item2 %in% M$id
  ) %>%
  group_by(item1) %>%
  top_n(-1, distance) %>%
  ungroup() %>%
  rename(D_j = distance) %>%
  select(-item2)

D_j

## # A tibble: 5 x 2
##   item1   D_j
##   <int> <dbl>
## 1     1 10.4 
## 2     2  8.25
## 3     3  2.83
## 4     5  1   
## 5     6  2.24

그리고 대표객체로 선정되지 않은 두 객체 \(i\), \(j\)에 대하여 다음을 산출한다.

\[\begin{equation*} C_{ji} = \max \left(D_j - d(j, i), 0\right) \end{equation*}\]

d_ji <- pairwise_distance_df %>%
  filter(
    !item1 %in% M$id,
    !item2 %in% M$id
  )

C_ji <- D_j %>%
  inner_join(d_ji, by = "item1") %>%
  mutate(C_ji = pmax(D_j - distance, 0))

C_ji

## # A tibble: 20 x 5
##    item1   D_j item2 distance  C_ji
##    <int> <dbl> <int>    <dbl> <dbl>
##  1     1 10.4      2     2.24 8.20 
##  2     1 10.4      3     9.43 1.01 
##  3     1 10.4      5    11.4  0    
##  4     1 10.4      6    12.6  0    
##  5     2  8.25     1     2.24 6.01 
##  6     2  8.25     3     7.21 1.04 
##  7     2  8.25     5     9.22 0    
##  8     2  8.25     6    10.4  0    
##  9     3  2.83     1     9.43 0    
## 10     3  2.83     2     7.21 0    
## 11     3  2.83     5     3.61 0    
## 12     3  2.83     6     4.12 0    
## 13     5  1        1    11.4  0    
## 14     5  1        2     9.22 0    
## 15     5  1        3     3.61 0    
## 16     5  1        6     1.41 0    
## 17     6  2.24     1    12.6  0    
## 18     6  2.24     2    10.4  0    
## 19     6  2.24     3     4.12 0    
## 20     6  2.24     5     1.41 0.822

이는 객체 \(i\)가 추가로 대표객체가 된다고 할 때, 객체 \(j\)의 입장에서 거리 감소량이다.

[단계 2] 다음과 같이 거리감소량이 가장 큰 객체 \(m\)을 대표객체에 포함시키고,

\[\begin{equation*} m = \arg\,\max_{i \notin M} \sum_{j \notin M} C_{ji} \end{equation*}\]

m <- C_ji %>%
  group_by(item2) %>%
  summarize(sum_C_ji = sum(C_ji)) %>%
  top_n(1, sum_C_ji) %>%
  .$item2

m

## [1] 2

대표객체집합을 수정한다.

\[\begin{equation*} M \leftarrow M \cup \{m\} \end{equation*}\]

M <- M %>%
  bind_rows(df[m, ])

[단계 3] \(K\)개의 대표객체가 선정되었으면 Stop, 그렇지 않은 경우에는 [단계 1]로 되돌아간다.

13.3.1.2.2 SWAP

SWAP은 대표객체로 선정되어 있는 객체 \(i\)와 선정되지 않은 객체 \(h\)를 교환할 때 목적함수의 변화량을 산출해 더 나은 목적함수값을 찾아가는 과정이다.

[단계 1] 객체 \(i\)와 객체 \(h\)를 교환할 때 목적함수의 변화량을 산출하기 위하여 우선, 대표객체로 선정되지 않은 임의의 객체 \(j \neq h\)에서의 변화량을 다음과 같이 산출한다.

\[\begin{eqnarray*} C_{jih} &=& \text{($i$와 $h$를 교환 후 객체 $j$와 대표객체와의 거리)}\\ & & - \text{(교환 전 객체 $j$와 대표객체와의 거리)},\\ & & \, (j \notin M, i \in M, h \notin M) \end{eqnarray*}\]

# 교환 전 각 객체와 대표 객체와의 거리
D_j <- pairwise_distance_df %>%
  filter(
    !item1 %in% M$id,
    item2 %in% M$id
  ) %>%
  group_by(item1) %>%
  top_n(-1, distance) %>%
  ungroup() %>%
  rename(j = item1) %>%
  select(-item2)

D_j

## # A tibble: 4 x 2
##       j distance
##   <int>    <dbl>
## 1     1     2.24
## 2     3     2.83
## 3     5     1   
## 4     6     2.24

# 교환할 객체
swap_ids <- tibble(
  i = rep(M$id, each = nrow(df) - nrow(M)),
  h = rep(setdiff(df$id, M$id), nrow(M))
)

# 교환 후 각 객체와 대표 객체와의 거리
update_distance <- function(i, h, distance_df, center_ids) {
  new_center_ids <- c(setdiff(center_ids, i), h)

  res <- distance_df %>%
    filter(
      !item1 %in% c(center_ids, h),
      item2 %in% new_center_ids
    ) %>%
    group_by(item1) %>%
    top_n(-1, distance) %>%
    ungroup() %>%
    rename(j = item1) %>%
    select(-item2) %>%
    mutate(
      i = i,
      h = h
    )
  
  return(res)
}

D_jih <- pmap_dfr(
  swap_ids, 
  update_distance,
  distance_df = pairwise_distance_df,
  center_ids = M$id
  )

D_jih

## # A tibble: 24 x 4
##        j distance     i     h
##    <int>    <dbl> <dbl> <dbl>
##  1     3     7.21     4     1
##  2     5     9.22     4     1
##  3     6    10.4      4     1
##  4     1     2.24     4     3
##  5     5     3.61     4     3
##  6     6     4.12     4     3
##  7     1     2.24     4     5
##  8     3     3.61     4     5
##  9     6     1.41     4     5
## 10     1     2.24     4     6
## # … with 14 more rows

# 거리의 변화량
C_jih <- D_j %>%
  inner_join(D_jih, by = "j", suffix = c("", "_new")) %>%
  mutate(diff_distance = distance_new - distance)

C_jih

## # A tibble: 24 x 6
##        j distance distance_new     i     h diff_distance
##    <int>    <dbl>        <dbl> <dbl> <dbl>         <dbl>
##  1     1     2.24         2.24     4     3         0    
##  2     1     2.24         2.24     4     5         0    
##  3     1     2.24         2.24     4     6         0    
##  4     1     2.24         9.43     2     3         7.20 
##  5     1     2.24        10.4      2     5         8.20 
##  6     1     2.24        10.4      2     6         8.20 
##  7     3     2.83         7.21     4     1         4.38 
##  8     3     2.83         3.61     4     5         0.777
##  9     3     2.83         4.12     4     6         1.29 
## 10     3     2.83         2.83     2     1         0    
## # … with 14 more rows

[단계 2] 대표객체 \(i\)를 \(h\)로 교환하는 경우 총 변화량은 다음과 같다.

\[\begin{equation*} T_{ih} = \sum_{j} C_{jih} \end{equation*}\]

T_ih <- C_jih %>%
  group_by(i, h) %>%
  summarize(total_diff_distance = sum(diff_distance))

## `summarise()` has grouped output by 'i'. You can override using the `.groups` argument.

T_ih

## # A tibble: 8 x 3
## # Groups:   i [2]
##       i     h total_diff_distance
##   <dbl> <dbl>               <dbl>
## 1     2     1              0     
## 2     2     3              7.20  
## 3     2     5              7.38  
## 4     2     6              8.20  
## 5     4     1             20.8   
## 6     4     3              4.49  
## 7     4     5             -0.0447
## 8     4     6              1.71

이 때 \(\min_{i, h} T_{ih}\)에 대응하는 객체 \(i^*\)와 \(h^*\)를 찾아 \(T_{i^*h^*} < 0\)이면 교환한 후에 다시 [단계 1]으로 돌아가고, \(T_{i^*h^*} \geq 0\)이면 교환하지 않고 stop.

swap_ih <- T_ih %>%
  filter(total_diff_distance < 0) %>%
  top_n(-1, total_diff_distance)

swap_ih

## # A tibble: 1 x 3
## # Groups:   i [1]
##       i     h total_diff_distance
##   <dbl> <dbl>               <dbl>
## 1     4     5             -0.0447

본 예제의 경우 객체 4 대신 객체 5가 새로운 대표객체로 선택되고, 다시 [단계 1]로 넘어간다.

M <- M %>%
  anti_join(df[swap_ih$i, ]) %>%
  bind_rows(df[swap_ih$h, ])

## Joining, by = c("id", "x1", "x2")

M

## # A tibble: 2 x 3
##      id    x1    x2
##   <dbl> <dbl> <dbl>
## 1     2     5     4
## 2     5    14     6

SWAP 과정이 종료된 후, 최종 군집해는 각 객체를 가장 가까운 대표객체가 속한 군집에 할당함으로써 얻어진다.

13.3.1.3 R 스크립트 구현

일련의 과정을 함수로 구현해보자.

# 각 객체로부터 가장 가까운 대표객체까지의 거리
distance_from_medoids <- function(distance_df, medoids_ids) {
  distance_df %>%
    filter(
      !item1 %in% medoids_ids,
      item2 %in% medoids_ids
    ) %>%
    group_by(item1) %>%
    arrange(distance) %>%
    slice(1) %>%
    ungroup() %>%
    rename(j = item1) %>%
    select(-item2)
}

# k개의 초기 대표객체를 선정
build_medoids <- function(distance_df, k = 1L) {
  k  <- min(k, length(unique(distance_df$item1)))

  # 첫 번째 대표객체 선정
  medoids_ids <- distance_df %>%
    group_by(item1) %>%
    summarize(sum_distance = sum(distance)) %>%
    arrange(sum_distance) %>%
    slice(1) %>%
    .$item1
  
  while (length(medoids_ids) < k) {
    D_j <- distance_from_medoids(distance_df, medoids_ids)

    d_ji <- distance_df %>%
      filter(
        !item1 %in% medoids_ids,
        !item2 %in% medoids_ids
      ) %>%
      rename(j = item1, i = item2)

    # 거리 감소량
    C_ji <- D_j %>%
      inner_join(d_ji, by = "j",
                 suffix = c("", "_new")) %>%
      mutate(diff_distance = pmax(distance - distance_new, 0))
    
    # 거리 감소량이 가장 큰 객체 선택
    m <- C_ji %>%
      group_by(i) %>%
      summarize(total_diff_distance = sum(diff_distance)) %>%
      arrange(desc(total_diff_distance)) %>%
      slice(1) %>%
      .$i
    
    # 대표객체에 추가
    medoids_ids <- c(medoids_ids, m)
  }
  
  return(medoids_ids)
}

# 교환 후 각 객체와 대표 객체와의 거리
update_distance <- function(i, h, distance_df, medoids_ids) {
  new_medoids_ids <- c(setdiff(medoids_ids, i), h)

  res <- distance_from_medoids(distance_df, new_medoids_ids) %>%
    filter(j != h) %>%
    mutate(
      i = i,
      h = h
    )

  return(res)
}

# 교환할 medoid 선택
swap_medoids <- function(distance_df, medoids_ids) {
  observation_ids <- unique(distance_df$item1)
  
  # 교환 전 각 객체와 대표 객체와의 거리
  D_j <- distance_from_medoids(distance_df, medoids_ids)
  
  # 교환할 객체
  swap_ids <- tibble(
    i = rep(medoids_ids, 
            each = length(observation_ids) - length(medoids_ids)),
    h = rep(setdiff(observation_ids, medoids_ids), 
            length(medoids_ids))
  )
  
  D_jih <- pmap_dfr(
    swap_ids, 
    update_distance,
    distance_df = distance_df,
    medoids_ids = medoids_ids
  )
  
  # 거리의 변화량
  C_jih <- D_j %>%
    inner_join(D_jih, by = "j", suffix = c("", "_new")) %>%
    mutate(diff_distance = distance_new - distance)
  
  T_ih <- C_jih %>%
    group_by(i, h) %>%
    summarize(total_diff_distance = sum(diff_distance))
  
  swap_ih <- T_ih %>%
    filter(total_diff_distance < 0) %>%
    arrange(total_diff_distance) %>%
    slice(1)
  
  return(list(remove = swap_ih$i, add = swap_ih$h))
}

# 전체 PAM 알고리즘
pam_medoids <- function(distance_df, k = 1L) {
  # BUILD
  medoids_ids <- build_medoids(distance_df, k)
  k <- length(medoids_ids)
  
  # SWAP
  while (TRUE) {
    swap_medoids <- swap_medoids(distance_df, medoids_ids)
    if (is_empty(swap_medoids$remove)) {
      break
    } else {
      medoids_ids <- c(
        setdiff(medoids_ids, swap_medoids$remove),
        swap_medoids$add
      )
    }
  }
  
  return (medoids_ids)
}

위 구현한 함수를 이용하여 아래와 같이 PAM을 실행해보자.

pairwise_distance_df <- dist(df[, -1], upper = TRUE) %>%
  broom::tidy() %>%
  mutate_if(is.factor, ~ as.integer(as.character(.)))

medoids_ids <- pam_medoids(pairwise_distance_df, k = 2)

## `summarise()` has grouped output by 'i'. You can override using the `.groups` argument.
## `summarise()` has grouped output by 'i'. You can override using the `.groups` argument.

df[medoids_ids, ]

## # A tibble: 2 x 3
##      id    x1    x2
##   <dbl> <dbl> <dbl>
## 1     2     5     4
## 2     5    14     6

위와 같이 2개의 대표객체 2, 5가 선정된다.

최종 군집해는 각 객체를 가장 가까운 대표객체가 속한 군집에 할당함으로써 얻어진다.

assign_cluster <- function(distance_df, medoids_ids) {
  distance_df %>%
    filter(
      !item1 %in% medoids_ids,
      item2 %in% medoids_ids
    ) %>%
    group_by(item1) %>%
    arrange(distance) %>%
    slice(1) %>%
    ungroup() %>%
    bind_rows(
      tibble(
        item1 = medoids_ids,
        item2 = medoids_ids,
        distance = 0
      )
    ) %>%
    rename(object = item1) %>%
    arrange(object) %>%
    group_by(item2) %>%
    mutate(cluster = str_c("{", str_c(object, collapse = ", "), "}")) %>%
    ungroup() %>%
    select(-item2)
}

assign_cluster(pairwise_distance_df, medoids_ids)

## # A tibble: 6 x 3
##   object distance cluster     
##    <int>    <dbl> <chr>       
## 1      1     2.24 {1, 2}      
## 2      2     0    {1, 2}      
## 3      3     3.61 {3, 4, 5, 6}
## 4      4     1    {3, 4, 5, 6}
## 5      5     0    {3, 4, 5, 6}
## 6      6     1.41 {3, 4, 5, 6}

13.3.2 CLARA 알고리즘

PAM 알고리즘은 SWAP 부분에서 모든 가능한 경우를 고려하기 때문에, 전체 객체 수가 많은 경우 계산 시간이 매우 길다는 단점이 있다. 이를 보완하기 위해 CLARA는 적절한 수의 객체를 샘플링한 후 이들에 대해 PAM 알고리즘을 적용하여 중심객체를 선정하는 방법이다. 이러한 샘플링을 여러 번 한 후, 이 중 가장 좋은 결과를 택하는 것인데, 반복수는 5번으로 충분한 것으로 분석되고 있다.

자세한 내용은 교재 (전치혁 2012) 참조

13.3.2.1 기본 R 스크립트

clara_solution <- cluster::clara(df[, -1], k = 2)

얻어진 clara 객체의 원소 i.med는 몇 번째 객체가 군집의 대표객체로 선정되었는지를 나타낸다.

clara_solution$i.med

## [1] 2 5

또한 clara 객체의 원소 clustering은 각 객체가 어떠한 군집에 할당되었는지를 보여준다.

clara_solution$clustering

## [1] 1 1 2 2 2 2

13.3.3 CLARANS 알고리즘

교재 (전치혁 2012) 참조

13.3.4 K-means-like 알고리즘

본 알고리즘은 PAM 알고리즘의 단점을 보완하고자 Park and Jun (2009) 에 의해 제안된 것으로, 대표객체를 반복적으로 수정하는데 K-means 알고리즘의 작동 원리를 모방한 K-medoids 군집 방법이다. 따라서 간단하며 계산 시간이 빠른 것이 장점이라 하겠다. 이 알고리즘은 다음과 같이 3단계로 구성되어 있다. 알고리즘의 각 단계를 Table 13.2의 예제 데이터에 적용하여 살펴보기로 하자.

[단계 1] (초기 대표객체 선정) \(K\)개의 초기 대표객체를 선정하며, 각 객체를 가장 가까운 대표객체에 배정하여 초기 군집해를 얻는다.

객체들 간의 거리 \(d(i, j), \, i, j = 1, \cdots, n\)를 구한다.

pairwise_distance_df <- dist(df[, -1], upper = TRUE) %>%
  broom::tidy() %>%
  mutate_if(is.factor, ~ as.integer(as.character(.)))

각 객체 \(j = 1, \cdots, n\)에 대하여 다음을 산출한다.

\[\begin{equation*} v_j = \sum_{i = 1}^{n} \frac{d(i, j)}{\sum_{k = 1}^{n} d(i, k)} \end{equation*}\]

v_j <- pairwise_distance_df %>%
  group_by(item2) %>%
  mutate(prop = distance / sum(distance)) %>%
  ungroup() %>%
  group_by(item1) %>%
  summarize(sum_prop = sum(prop)) %>%
  rename(j = item1)

v_j

## # A tibble: 6 x 2
##       j sum_prop
##   <int>    <dbl>
## 1     1    1.67 
## 2     2    1.33 
## 3     3    0.781
## 4     4    0.661
## 5     5    0.713
## 6     6    0.849

이후 \(v_j\)값들을 오름차순으로 정렬하여 가장 작은 \(K\)개의 값을 초기 대표객체로 선정한다. 본 예에서는 \(K = 2\)로 가정하자.

medoids_ids <- v_j %>%
  arrange(sum_prop) %>%
  slice(1:2) %>%
  .$j

medoids_ids

## [1] 4 5

이후 객체를 배정하여 군집해를 얻는다. 위에서 정의했던 assign_cluster 함수를 재사용하자.

cluster_solution <- assign_cluster(
  pairwise_distance_df, 
  medoids_ids
  )

cluster_solution

## # A tibble: 6 x 3
##   object distance cluster     
##    <int>    <dbl> <chr>       
## 1      1    10.4  {1, 2, 3, 4}
## 2      2     8.25 {1, 2, 3, 4}
## 3      3     2.83 {1, 2, 3, 4}
## 4      4     0    {1, 2, 3, 4}
## 5      5     0    {5, 6}      
## 6      6     1.41 {5, 6}

[단계 2] (대표객체의 수정) 현재의 군집에 배정된 객체들의 대표객체를 구하여 새로운 대표객체로 삼는다. 새로운 대표객체는 같은 군집에 배정된 다른 객체들로부터의 거리의 합이 최소가 되는 객체이다.

find_medoids <- function(distance_df, ids) {
  distance_df %>%
    filter(
      item1 %in% ids, 
      item2 %in% ids
      ) %>%
    group_by(item1) %>%
    summarize(total_distance = sum(distance)) %>%
    arrange(total_distance) %>%
    slice(1) %>%
    .$item1
}

cluster_objects <- cluster_solution %>%
  split(.$cluster) %>%
  map(~.$object)

medoids_ids <- map_int(
  cluster_objects, 
  find_medoids,
  distance_df = pairwise_distance_df
)

medoids_ids

## {1, 2, 3, 4}       {5, 6} 
##            2            5

[단계 3] (객체의 배정) 각 객체를 가장 가까운 대표객체에 배정하여 군집해를 얻는다. 군집해가 이전과 동일하면 Stop하고, 그렇지 않으면 [단계 2]를 반복한다.

new_cluster_solution <- assign_cluster(
  pairwise_distance_df, 
  medoids_ids
  )

is_converge <- near(
  1, 
  # clusteval::cluster_similarity(
  #   as.factor(cluster_solution$cluster),
  #   as.factor(new_cluster_solution$cluster),
  #   similarity = "rand"
  # )
  flexclust::randIndex(
    as.factor(cluster_solution$cluster),
    as.factor(new_cluster_solution$cluster)
  )
)

print(is_converge)

##   ARI 
## FALSE

위의 경우 첫 번째 iteration에서 군집해가 수정되었으므로 다음 iteration을 수행한다.

13.3.4.1 R 스크립트 구현

위 일련의 과정들을 수행하는 R 함수 스크립트를 구현해보자.

init_medoids <- function(distance_df, k = 1) {
  object_ids <- unique(distance_df$item1)
  k <- min(k, length(object_ids))
  
  v_j <- distance_df %>%
    group_by(item2) %>%
    mutate(prop = distance / sum(distance)) %>%
    ungroup() %>%
    group_by(item1) %>%
    summarize(sum_prop = sum(prop)) %>%
    rename(j = item1)
  
  medoids_ids <- v_j %>%
    arrange(sum_prop) %>%
    slice(1:k) %>%
    .$j
  
  return(medoids_ids)
}

assign_cluster <- function(distance_df, medoids_ids) {
  distance_df %>%
    filter(
      !item1 %in% medoids_ids,
      item2 %in% medoids_ids
    ) %>%
    group_by(item1) %>%
    arrange(distance) %>%
    slice(1) %>%
    ungroup() %>%
    bind_rows(
      tibble(
        item1 = medoids_ids,
        item2 = medoids_ids,
        distance = 0
      )
    ) %>%
    rename(object = item1) %>%
    arrange(object) %>%
    group_by(item2) %>%
    mutate(cluster = str_c("{", str_c(object, collapse = ", "), "}")) %>%
    ungroup() %>%
    select(-item2)
}

find_medoids <- function(distance_df, ids) {
  distance_df %>%
    filter(
      item1 %in% ids, 
      item2 %in% ids
      ) %>%
    group_by(item1) %>%
    summarize(total_distance = sum(distance)) %>%
    arrange(total_distance) %>%
    slice(1) %>%
    .$item1
}

kmeans_like_kmedoids <- function(distance_df, k = 1) {
  medoids_ids <- init_medoids(distance_df, k)
  
  while (TRUE) {
    cluster_solution <- assign_cluster(distance_df, medoids_ids)
    
    cluster_objects <- cluster_solution %>%
      split(.$cluster) %>%
      map(~.$object)
    
    medoids_ids <- map_int(
      cluster_objects, 
      find_medoids,
      distance_df = distance_df
    )
    
    new_cluster_solution <- assign_cluster(distance_df, medoids_ids)
    
    is_converge <- near(
      1, 
      flexclust::randIndex(
        as.factor(cluster_solution$cluster),
        as.factor(new_cluster_solution$cluster)
      )
    )
    
    if (is_converge) break
  }
  
  return(medoids_ids)
}

위에서 정의한 함수 kmeans_like_kmedoids를 Table 13.2의 데이터에 적용한 군집결과 및 군집 대표객체는 아래와 같이 얻어진다.

pairwise_distance_df <- dist(df[, -1], upper = TRUE) %>%
  broom::tidy() %>%
  mutate_if(is.factor, ~ as.integer(as.character(.)))

medoids_ids <- kmeans_like_kmedoids(pairwise_distance_df, k = 2)

medoids_ids

##       {1, 2} {3, 4, 5, 6} 
##            1            5

13.4 퍼지 K-means 알고리즘

이 방법은 K-means 알고리즘과 유사하나, 하나의 객체가 여러 군집에 속할 가능성을 허용하는 확률 또는 이를 확장한 퍼지(fuzzy) 개념을 도입한 것이다. 객체 \(i\)가 군집 \(j\)에 속할 확률 \(P_{ij}\)를 구하는 문제이다.

13.4.1 기본 R 스크립트

df <- tibble(
  id = c(1:10),
  x1 = c(6, 8, 14, 11, 15, 7, 13, 5, 3, 3),
  x2 = c(14, 13, 6, 8, 7, 15, 6, 4, 3, 2)
)

df %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r'),
    col.names = c(
      '객체번호', 
      '사용경력($x_1$)', 
      '사용시간($x_2$)'
      ),
    caption = 'PC 사용자 데이터'
  )

Table 13.3: PC 사용자 데이터

객체번호	사용경력(\(x_1\))	사용시간(\(x_2\))
1	6	14
2	8	13
3	14	6
4	11	8
5	15	7
6	7	15
7	13	6
8	5	4
9	3	3
10	3	2

cluster::fanny(df[, -1], k = 3, metric = "SqEuclidean")

## Fuzzy Clustering object of class 'fanny' :                      
## m.ship.expon.        2
## objective     18.37061
## tolerance        1e-15
## iterations          12
## converged            1
## maxit              500
## n                   10
## Membership coefficients (in %, rounded):
##       [,1] [,2] [,3]
##  [1,]   98    1    1
##  [2,]   96    3    2
##  [3,]    1   99    1
##  [4,]   12   80    8
##  [5,]    2   96    2
##  [6,]   98    1    1
##  [7,]    1   99    1
##  [8,]    3    3   94
##  [9,]    0    0   99
## [10,]    1    1   98
## Fuzzyness coefficients:
## dunn_coeff normalized 
##  0.9225653  0.8838480 
## Closest hard clustering:
##  [1] 1 1 2 2 2 1 2 3 3 3
## 
## Available components:
##  [1] "membership"  "coeff"       "memb.exp"   
##  [4] "clustering"  "k.crisp"     "objective"  
##  [7] "convergence" "diss"        "call"       
## [10] "silinfo"     "data"

13.4.2 알고리즘

[단계 0] 초기 \(K\)개의 군집을 임의로 결정한다.

\[\begin{equation*} P_{ij} = \begin{cases} 1 & \text{ if object $i$ belongs to cluster $j$}\\ 0 & \text{ otherwise} \end{cases} \end{equation*}\]

init_cluster <- function(df, k = 1) {
  k <- min(k, nrow(df))
  
  while (TRUE) {
    cluster_ind <- sample.int(k, size = nrow(df), replace = TRUE)
    if (length(unique(cluster_ind)) == k) break
  }
  
  map_dfc(unique(cluster_ind), ~ as.double(cluster_ind == .))
}

set.seed(4000)

cluster_membership <- init_cluster(df[, -1], k = 3)

## New names:
## * NA -> ...1
## * NA -> ...2
## * NA -> ...3

cluster_membership

## # A tibble: 10 x 3
##     ...1  ...2  ...3
##    <dbl> <dbl> <dbl>
##  1     1     0     0
##  2     1     0     0
##  3     0     1     0
##  4     1     0     0
##  5     0     0     1
##  6     0     1     0
##  7     0     0     1
##  8     0     1     0
##  9     1     0     0
## 10     1     0     0

[단계 1] 각 군집의 중심좌표를 산출한다.

\[\begin{equation*} \mathbf{c}_j = \frac{\sum_{i = 1}^{n} P_{ij}^{m} \mathbf{x}_i}{\sum_{i = 1}^{n} P_{ij}^{m}} \end{equation*}\]

여기에서 상수 \(m\)은 1보다 큰 값을 사용한다.

find_center <- function(df, p, m) {
  wt <- p ^ m
  df %>% 
    summarize_all(weighted.mean, w = wt)
}

cluster_df <- map_dfr(cluster_membership, find_center, df = df[, -1], m = 2)

cluster_df

## # A tibble: 3 x 2
##      x1    x2
##   <dbl> <dbl>
## 1  6.2   8   
## 2  8.67  8.33
## 3 14     6.5

[단계 2] 군집 membership 계수 \(P_{ij}\)를 업데이트한다.

\[\begin{equation*} P_{ij} = \frac{d(\mathbf{x}_i, \mathbf{c}_j)^{-\frac{1}{m - 1}}}{\sum_{a = 1}^{K} d(\mathbf{x}_i, \mathbf{c}_a)^{-\frac{1}{m - 1}}} \end{equation*}\]

여기에서 거리함수 \(d()\)는 제곱 유클리드 거리를 사용한다.

update_membership <- function(df, cluster_df, m) {
  distance_mat <- flexclust::dist2(df, cluster_df)  ^ 2
  
  p <- distance_mat ^ (-1 / (m - 1)) %>%
    `/`(rowSums(.)) %>%
    as_tibble(.name_repair = "minimal")
  
  p
}

update_membership(df[, -1], cluster_df, m = 2)

## # A tibble: 10 x 3
##         ``      ``    ``
##      <dbl>   <dbl> <dbl>
##  1 0.451   0.414   0.135
##  2 0.380   0.483   0.137
##  3 0.00381 0.00730 0.989
##  4 0.139   0.576   0.285
##  5 0.0152  0.0285  0.956
##  6 0.406   0.427   0.166
##  7 0.0231  0.0479  0.929
##  8 0.574   0.311   0.115
##  9 0.542   0.315   0.143
## 10 0.508   0.325   0.166

13.4.3 R 스크립트 구현

fuzzy_kmeans <- function(df, k = 1, m = 2, max_iter = 1000L, tol = 1e-9) {
  k <- min(k, nrow(df))
  i <- 0L
  
  cluster_membership <- init_cluster(df, k)
  
  while (i < max_iter) {
    i <- i + 1L
    
    cluster_df <- map_dfr(cluster_membership, find_center, df = df, m = m)
    
    new_cluster_membership <- update_membership(df, cluster_df, m)
    
    if (max(abs(cluster_membership - new_cluster_membership)) < tol) break
    
    cluster_membership <- new_cluster_membership
  }
  
  res <- list(
    n_iteration = i,
    center = cluster_df,
    membership = cluster_membership %>% as.matrix()
  )
  
  return (res)
}

set.seed(4000)

fuzzy_kmeans_solution <- fuzzy_kmeans(df[, -1], k = 3, m = 2)

## New names:
## * NA -> ...1
## * NA -> ...2
## * NA -> ...3

fuzzy_kmeans_solution$n_iteration

## [1] 16

fuzzy_kmeans_solution$center

## # A tibble: 3 x 2
##      x1    x2
##   <dbl> <dbl>
## 1  3.64  2.98
## 2  7.00 14.0 
## 3 13.4   6.63

fuzzy_kmeans_solution$membership

##                                          
##  [1,] 0.007809655 0.983147737 0.009042608
##  [2,] 0.015726915 0.957515486 0.026757600
##  [3,] 0.006068358 0.006268614 0.987663029
##  [4,] 0.078772454 0.120672309 0.800555237
##  [5,] 0.017165082 0.022105992 0.960728926
##  [6,] 0.006532987 0.984345339 0.009121674
##  [7,] 0.005945712 0.005766360 0.988287928
##  [8,] 0.939278603 0.026072757 0.034648640
##  [9,] 0.993661877 0.002989486 0.003348637
## [10,] 0.981125198 0.008481303 0.010393499

fuzzy_kmeans_solution$membership %>%
  apply(1, which.max)

##  [1] 2 2 3 3 3 2 3 1 1 1

13.5 모형기반 군집방법

모형기반 군집방법(model-based clustering)에서는 각 객체가 혼합분포(mixture)를 따른다고 가정하여 객체의 군집배정변수를 통계적으로 추정하는 것이다.

13.5.1 기본 R script

df <- tibble(
  id = c(1:7),
  x1 = c(4, 6, 6, 10, 11, 12, 12),
  x2 = c(12, 13, 15, 4, 3, 2, 5)
)

df %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r'),
    col.names = c(
      '객체번호', 
      '$x_1$', 
      '$x_2$'
      ),
    caption = '모형기반 군집 학습 데이터'
  )

Table 13.4: 모형기반 군집 학습 데이터

객체번호	\(x_1\)	\(x_2\)
1	4	12
2	6	13
3	6	15
4	10	4
5	11	3
6	12	2
7	12	5

Table 13.4의 7개의 객체를 두 개의 군집에 배정하는 간단한 R 스크립트는 아래와 같다. 여기에서 mclust::meVII는 각 군집의 분산-공분산 행렬은 서로 다르되, 각 변수의 분산이 동일하며 공분산은 0이라 가정한다.

set.seed(1024)

# 군집 개수
K <- 2

# z_ik 값 초기화
init_z <- matrix(runif(nrow(df) * K), ncol = K) %>%
  `/`(apply(., 1, sum))

# EM 알고리즘 - 분산-공분산 행렬: unequal volume (V), spherical(II) 
sol <- mclust::meVII(data = df[, -1], z = init_z)

# 군집 사후확률
sol$z

##              [,1]         [,2]
## [1,] 7.596402e-28 1.000000e+00
## [2,] 8.254183e-27 1.000000e+00
## [3,] 9.463816e-36 1.000000e+00
## [4,] 1.000000e+00 6.832084e-20
## [5,] 1.000000e+00 1.473491e-25
## [6,] 1.000000e+00 4.876251e-31
## [7,] 1.000000e+00 1.480388e-20

# 혼합분포
sol$parameters

## $pro
## [1] 0.5714286 0.4285714
## 
## $mean
##     [,1]      [,2]
## x1 11.25  5.333333
## x2  3.50 13.333333
## 
## $variance
## $variance$modelName
## [1] "VII"
## 
## $variance$d
## [1] 2
## 
## $variance$G
## [1] 2
## 
## $variance$sigma
## , , 1
## 
##         x1      x2
## x1 0.96875 0.00000
## x2 0.00000 0.96875
## 
## , , 2
## 
##          x1       x2
## x1 1.222222 0.000000
## x2 0.000000 1.222222
## 
## 
## $variance$sigmasq
## [1] 0.968750 1.222222
## 
## $variance$scale
## [1] 0.968750 1.222222
## 
## 
## $Vinv
## NULL

13.5.2 EM 알고리즘

우선, 필요한 기호를 다음과 같이 정의하자.

• \(f_k(\mathbf{x} \, | \, \theta_k)\): 군집 \(k\)에 속하는 객체 \(\mathbf{x}\)의 확률밀도함수(\(\theta_k\)는 관련 파라미터)
• \(\tau_k\): 임의의 객체가 군집 \(k\)에 속할 사전확률 (\(\tau_k \geq 0, \, \sum_{k = 1}^{K} \tau = 1\))

이 때, 임의의 객체 \(\mathbf{x}\)는 다음과 같은 혼합 확률밀도함수를 갖는다.

\[\begin{equation*} f(\mathbf{x} \, | \, \boldsymbol\theta) = \sum_{k = 1}^{K} \tau_k f_k(\mathbf{x} \, | \, \theta_k) \end{equation*}\]

본 장에서는 \(f_k\)가 다변량 정규분포를 나타낸다고 가정하자.

추가로, 각 객체가 속하는 군집에 대한 지시변수 \(z_{ik}\)를 아래와 같이 정의하자.

\[\begin{equation*} z_{ik} = \begin{cases} 1 & \text{ if object $i$ belongs to cluster $k$} \\ 0 & \text{ otherwise} \end{cases} \end{equation*}\]

이 \(z_{ik}\) 변수는 실제값이 관측되지 않는 변수이므로, 최우추정법을 이용하여 그 기대값, 즉 객체 \(i\)가 군집 \(k\)에 속할 확률을 추정한다. 보다 자세한 설명은 교재 (전치혁 2012) 참조.

앞의 13.5.1장에서 수행했던 예제를 단계별로 살펴보기로 하자.

[단계 0] \(\hat{z}_{ik}\)를 초기화한다.

set.seed(1024)

# 군집 개수
K <- 2

# z_ik 추정값 초기화
z_hat <- matrix(runif(nrow(df) * K), ncol = K) %>%
  `/`(apply(., 1, sum)) %>%
  as_tibble() %>%
  `names<-`(str_c("C", 1:K))

z_hat

## # A tibble: 7 x 2
##       C1     C2
##    <dbl>  <dbl>
## 1 0.406  0.594 
## 2 0.623  0.377 
## 3 0.372  0.628 
## 4 0.956  0.0444
## 5 0.0214 0.979 
## 6 0.681  0.319 
## 7 0.264  0.736

[단계 1] (M-step) \(\hat{z}_{ik}\)를 바탕으로 파라미터를 추정한다.

우선 \(\tau_k\)와 \(\boldsymbol\mu_k\)를 다음과 같이 추정한다.

\[\begin{equation*} \hat{\tau}_k = \frac{\sum_{i = 1}^{n} \hat{z}_{ik}}{n} \end{equation*}\]

tau_hat <- map(z_hat, mean)
tau_hat

## $C1
## [1] 0.4746762
## 
## $C2
## [1] 0.5253238

\[\begin{equation*} \hat{\boldsymbol\mu}_k = \frac{\sum_{i = 1}^{n} \hat{z}_{ik} \mathbf{x}_i}{\sum_{i = 1}^{n} \hat{z}_{ik}} \end{equation*}\]

mu_hat <- map(z_hat, ~colSums(.*df[, -1]) / sum(.))
mu_hat

## $C1
##       x1       x2 
## 8.644042 7.559792 
## 
## $C2
##       x1       x2 
## 8.777757 7.853884

분산-공분산 행렬 \(\boldsymbol\Sigma_k\)의 추정은 분산-공분산 구조를 어떻게 가정하느냐에 따라 다르다. 우선, 일반적으로 분산-공분산 행렬 \(\boldsymbol\Sigma_k\)는 아래와 같이 decompose할 수 있다 (Banfield and Raftery 1993).

\[\begin{equation*} \boldsymbol\Sigma_k = \lambda_k \mathbf{D}_k \mathbf{A}_k \mathbf{D}_k^\top \end{equation*}\]

여기에서

• \(\lambda_k = \det{\boldsymbol\Sigma_k}^{1 / 2}\); 군집 \(k\)이 크기와 관련
• \(\mathbf{D}_k\): matrix of eigenvectors of \(\boldsymbol\Sigma_k\); 군집 \(k\)의 방향(orientation)과 관련
• \(\mathbf{A}_k\): diagonal matrix s.t. \(\det{\mathbf{A}_k} = 1\); 군집 \(k\)의 형태와 관련

이다. \(\lambda_k\), \(\mathbf{D}_k\) 및 \(\mathbf{A}_k\)에 적용되는 제약조건에 따라 분산-공분산 모형을 정의할 수 있다. 아래는 본 장에서 다룰 세 가지 모형이다.

tribble(
  ~model, ~sigma,
  "VII", "$\\lambda_k \\mathbf{I}$",
  "VEI", "$\\lambda_k \\mathbf{A}$",
  "VEE", "$\\lambda_k \\mathbf{D} \\mathbf{A} \\mathbf{D}^\\top$"
) %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('c', 'c'),
    col.names = c(
      '분산-공분산 모형', 
      '$\\boldsymbol\\Sigma_k$'
      ),
    caption = 'Within-group 분산-공분산 모형'
  )

Table 13.5: Within-group 분산-공분산 모형

분산-공분산 모형	\(\boldsymbol\Sigma_k\)
VII	\(\lambda_k \mathbf{I}\)
VEI	\(\lambda_k \mathbf{A}\)
VEE	\(\lambda_k \mathbf{D} \mathbf{A} \mathbf{D}^\top\)

즉,

• “VII”
  • for all \(k\),\(\mathbf{D}_k = \mathbf{I}\)
  • for all \(k\), \(\mathbf{A}_k = \mathbf{I}\)
• “VEI”
  • for all \(k\), \(\mathbf{D}_k = \mathbf{I}\)
  • for all \(k\), \(\mathbf{A}_k = \mathbf{A}\)
• “VEE”
  • for all \(k\), \(\mathbf{D}_k = \mathbf{D}\)
  • for all \(k\), \(\mathbf{A}_k = \mathbf{A}\)

Celeux and Govaert (1995) 에 각 분산-공분산 모형에 대한 추정값을 얻는 반복적 알고리즘이 소개되어 있으며, 이는 교재 (전치혁 2012)에도 설명되어 있다.

우선, 각 군집 \(k\) 내에서의 scatter matrix를 아래와 같이 계산한다.

\[\begin{equation*} \mathbf{W}_k = \sum_{i = 1}^{n} \hat{z}_{ik} (\mathbf{x}_i - \hat{\boldsymbol\mu}_k)(\mathbf{x}_i - \hat{\boldsymbol\mu}_k)^\top \end{equation*}\]

p <- ncol(df[, -1])
W <- map(mu_hat, 
    ~pmap_dfc(list(x = df[, -1], mu = .),
             function(x, mu) x - mu)) %>%
  map(as.matrix, nrow = p, ncol = p) %>%
  map2(z_hat, ~ t(.x) %*% (.y * .x))

W

## $C1
##           x1        x2
## x1  28.22794 -44.46516
## x2 -44.46516  82.36848
## 
## $C2
##           x1        x2
## x1  37.16942 -53.17491
## x2 -53.17491  92.90912

이후 분산-공분산 모형에 따라 아래와 같이 각 군집의 분산-공분산 행렬을 추정한다.

[VII의 경우] 반복 업데이트의 과정 없이 closed-form으로 해가 존재한다.

\[\begin{equation*} \lambda_k = \frac{Tr(\mathbf{W}_k)}{p \sum_{i = 1}^{n} \hat{z}_{ik}} \end{equation*}\]

\[\begin{equation*} \boldsymbol\Sigma_k = \lambda_k \mathbf{I} \end{equation*}\]

이 때 \(p\)는 관측값의 차원수이다 (\(\mathbf{x} \in \mathbb{R}^p\)).

[VEI의 경우]

VEI-0. 행렬 \(\mathbf{B} = \mathbf{I}\)로 초기화한다.

VEI-1. \(\lambda_k\)값을 아래와 같이 계산한다.

\[\begin{equation*} \lambda_k = \frac{Tr(\mathbf{W}_k \mathbf{B}^{-1})}{p \sum_{i = 1}^{n} \hat{z}_{ik}} \end{equation*}\]

VEI-2. 행렬 \(\mathbf{B}\)를 아래와 같이 업데이트한다.

\[\begin{equation*} \mathbf{B} = \frac{diag\left( \sum_{k = 1}^{K} \frac{\mathbf{W}_k}{\lambda_k} \right)}{\left( \det diag\left( \sum_{k = 1}^{K} \frac{\mathbf{W}_k}{\lambda_k} \right) \right)^{1 / p}} \end{equation*}\]

VEI-3. 결과가 수렴하면 종료, 그렇지 않으면 VEI-1로 돌아간다. 최종 수렴한 결과를 통해 각 군집의 분산-공분산 행렬을 아래와 같이 얻는다.

\[\begin{equation*} \boldsymbol\Sigma_k = \lambda_k \mathbf{B} \end{equation*}\]

[VEE의 경우]

VEE-0. 행렬 \(\mathbf{C} = \mathbf{I}\)로 초기화한다.

VEE-1. \(\lambda_k\)값을 아래와 같이 계산한다.

\[\begin{equation*} \lambda_k = \frac{Tr(\mathbf{W}_k \mathbf{C}^{-1})}{p \sum_{i = 1}^{n} \hat{z}_{ik}} \end{equation*}\]

VEE-2. 행렬 \(\mathbf{C}\)를 아래와 같이 업데이트한다.

\[\begin{equation*} \mathbf{C} = \frac{\sum_{k = 1}^{K} \frac{\mathbf{W}_k}{\lambda_k}}{\left( \det \sum_{k = 1}^{K} \frac{\mathbf{W}_k}{\lambda_k} \right)^{1 / p}} \end{equation*}\]

VEE-3. 결과가 수렴하면 종료, 그렇지 않으면 VEE-1로 돌아간다. 최종 수렴한 결과를 통해 각 군집의 분산-공분산 행렬을 아래와 같이 얻는다.

\[\begin{equation*} \boldsymbol\Sigma_k = \lambda_k \mathbf{C} \end{equation*}\]

위 각 분산-공분산 모형을 추정 과정에 대한 설명은, 보다 일반화된 분산-공분산 구조 \(\lambda_k \mathbf{D}_k \mathbf{A}_k \mathbf{D}_k^\top\)을 추정하는 과정을 각 모형에 추가되는 제약에 따라 조금 더 단순하게 표현한 것이다. 보다 자세한 내용은 Celeux and Govaert (1995) 참조.

아래와 같이 군집 내 분산-공분산 행렬을 추정하는 함수 estimate_mixture_cov를 구현해보자. 해당 함수는 3개의 입력변수를 사용한다.

• modelName: 분산-공분산 모형 이름. “VII”, “VEI”, “VEE” 중 하나를 선택한다.
• W: K개의 scatter matrix (\(\mathbf{W}_1, \cdots, \mathbf{W}_K\))를 원소로 지니는 리스트 (list)
• z: \(z_{ik}\) 값을 지닌 데이터 프레임 (data.frame). \(n\)개의 행과 \(K\)개의 열로 이루어진다. 즉, 행은 각 관측객체를 나타내며, 열은 각 군집을 나타낸다.

estimate_mixture_cov <- function(modelName, W, z) {
  K <- ncol(z)
  p <- ncol(W[[1]])

  # 초기화
  D <- map(1:K, ~ diag(1, p))
  A <- map(1:K, ~ diag(1, p))
  
  get_lambda <- function(W, z, D, A, p) {
    pmap(
      list(W, z, D, A),
      function(W, z, D, A, p)
        sum(diag(W %*% D %*% solve(A) %*% t(D))) / (sum(z) * p),
      p = p
      )
  }
  
  objective_value <- function(W, z, lambda, D, A, p) {
    pmap_dbl(
      list(W, z, lambda, D, A),
      function(W, z, lambda, D, A, p)
        sum(diag(W %*% D %*% solve(A) %*% t(D))) / lambda +
        p * sum(z) * log(lambda),
      p = p
    ) %>%
      sum()
  }
  
  i <- 0L
  obj <- Inf
  
  while(TRUE) {
    i <- i + 1L
    
    lambda <- get_lambda(W, z, D, A, p)
    new_obj <- objective_value(W, z, lambda, D, A, p)
    
    if (obj - new_obj < 1e-9) break
    
    if (modelName == "VII") {
      
    } else if (modelName == "VEI") {
      B <- map2(W, lambda, ~ diag(.x) / .y) %>% 
        reduce(`+`) %>%
        diag() %>%
        `/`(det(.) ^ (1 / p))
      A <- map(1:K, ~ B)
    } else if (modelName == "VEE") {
      C <- map2(W, lambda, ~ .x / .y) %>% 
        reduce(`+`) %>%
        `/`(det(.) ^ (1 / p))
      
      s <- svd(C)
      A <- map(1:K, ~ diag(s$d))
      D <- map(1:K, ~ s$u)
    } else {
      stop("Model ", modelName, " is not supported yet.")
    }
    
    obj <- new_obj
  }

  Sigma <- pmap(
    list(lambda, D, A),
    function(lambda, D, A) lambda * (D %*% A %*% t(D))
    )

  return (list(
    volume = lambda,
    shape = A,
    orientation = D,
    Sigma = Sigma
  ))
}

초기값으로 주어진 \(\hat{z}_{ik}\) 를 이용하여 “VII” 구조의 분산-공분산 행렬을 구해보자.

estimate_mixture_cov("VII", W, z_hat)

## $volume
## $volume$C1
## [1] 16.64239
## 
## $volume$C2
## [1] 17.68685
## 
## 
## $shape
## $shape[[1]]
##      [,1] [,2]
## [1,]    1    0
## [2,]    0    1
## 
## $shape[[2]]
##      [,1] [,2]
## [1,]    1    0
## [2,]    0    1
## 
## 
## $orientation
## $orientation[[1]]
##      [,1] [,2]
## [1,]    1    0
## [2,]    0    1
## 
## $orientation[[2]]
##      [,1] [,2]
## [1,]    1    0
## [2,]    0    1
## 
## 
## $Sigma
## $Sigma$C1
##          [,1]     [,2]
## [1,] 16.64239  0.00000
## [2,]  0.00000 16.64239
## 
## $Sigma$C2
##          [,1]     [,2]
## [1,] 17.68685  0.00000
## [2,]  0.00000 17.68685

위 estimate_mixture_cov 함수에서 “VII”보다 일반화된 “VEI”와 “VEE” 분산-공분산 모형에 대한 추정도 구현되어 있다.

# estimate_mixture_cov("VEI", W, z_hat)
# estimate_mixture_cov("VEE", W, z_hat)

위 일련의 파리미터 추정을 하나의 함수 GMM_Mstep으로 아래와 같이 구성해보자.

GMM_Mstep <- function(df, z, modelName = "VII") {
  tau <- map(z, mean)
  mu <- map(z, ~colSums(. * df) / sum(.))
  
  p <- ncol(df)
  W <- map(mu, ~pmap_dfc(
    list(x = df, mu = .), function(x, mu) x - mu)) %>%
  map(as.matrix, nrow = p, ncol = p) %>%
  map2(z, ~ t(.x) %*% (.y * .x))
  
  var_cov <- estimate_mixture_cov(modelName, W, z)
  
  res <- list(
    tau = tau,
    mu = mu,
    Sigma = var_cov$Sigma
  )
  
  return (res)
}

Mstep_res <- GMM_Mstep(df[, -1], z_hat)

Mstep_res

## $tau
## $tau$C1
## [1] 0.4746762
## 
## $tau$C2
## [1] 0.5253238
## 
## 
## $mu
## $mu$C1
##       x1       x2 
## 8.644042 7.559792 
## 
## $mu$C2
##       x1       x2 
## 8.777757 7.853884 
## 
## 
## $Sigma
## $Sigma$C1
##          [,1]     [,2]
## [1,] 16.64239  0.00000
## [2,]  0.00000 16.64239
## 
## $Sigma$C2
##          [,1]     [,2]
## [1,] 17.68685  0.00000
## [2,]  0.00000 17.68685

[단계 2] (E-step) M-step에서의 파라미터 추정치를 바탕으로 \(\hat{z}_{ik}\)를 산출한다.

\[\begin{equation*} \hat{z}_{ik} = \frac{\hat{\tau}_k f_k(\mathbf{x}_i \, | \, \hat{\boldsymbol{\mu}}_k, \hat{\boldsymbol{\Sigma}}_k)}{\sum_{l = 1}^{K} \hat{\tau}_l f_l(\mathbf{x}_i \, | \, \hat{\boldsymbol{\mu}}_l, \hat{\boldsymbol{\Sigma}}_l)} \end{equation*}\]

GMM_Estep <- function(df, tau, mu, Sigma) {
  pmap_dfc(list(tau = tau, mu = mu, Sigma = Sigma),
       function(df, tau, mu, Sigma) 
         tau * mvtnorm::dmvnorm(df, mean = mu, sigma = Sigma),
       df = df) %>%
    `/`(rowSums(.))
}

new_z_hat <- GMM_Estep(df[, -1], Mstep_res$tau, Mstep_res$mu, Mstep_res$Sigma)

new_z_hat

##          C1        C2
## 1 0.4626878 0.5373122
## 2 0.4568716 0.5431284
## 3 0.4373551 0.5626449
## 4 0.4964082 0.5035918
## 5 0.4934276 0.5065724
## 6 0.4886741 0.5113259
## 7 0.4870085 0.5129915

[단계 3] 수렴조건을 만족하면 stop, 그렇지 않으면 [단계 1]을 반복한다. 일반적으로는 우도함수값의 변화량을 수렴조건으로 사용하나, 본 장에서는 간단하게 \(z_{ik}\)값의 변화량을 기준으로 수렴을 판단하도록 하자.

max(abs(z_hat - new_z_hat)) < 1e-9

## [1] FALSE

위 수식의 값이 TRUE이면 수렴, FALSE이면 [단계 1]을 반복한다.

13.5.3 R 스크립트 구현

위 일련의 과정들을 포함하는 하나의 함수 GMM_EM을 아래와 같이 구현해보자. 앞에서 정의했던 함수 GMM_Mstep 및 GMM_Estep을 재사용한다.

GMM_EM <- function(df, K, modelName = "VII", tol = 1e-9) {
  K <- min(K, nrow(df))
  
  i <- 0L  
  
  # [단계 0] z_ik 추정값 초기화
  z_hat <- matrix(runif(nrow(df) * K), ncol = K) %>%
    `/`(apply(., 1, sum)) %>%
    as_tibble() %>%
    `names<-`(str_c("C", 1:K))
  
  while (TRUE) {
    i <- i + 1L
    
    # [단계 1] M-step
    Mstep_res <- GMM_Mstep(df, z_hat, modelName)
    
    # [단계 2] E-step
    new_z_hat <- GMM_Estep(df, Mstep_res$tau, Mstep_res$mu, Mstep_res$Sigma)
    
    # [단계 3] 수렴조건 확인
    if (max(abs(z_hat - new_z_hat)) < tol) break
    
    z_hat <- new_z_hat
  }
  
  return (list(z = z_hat, 
               parameters = Mstep_res,
               n_iteration = i))
}

위 함수를 학습데이터 Table 13.4에 적용한 결과는 아래와 같다.

VII_res <- GMM_EM(df[, -1], 2, "VII")

# 군집 멤버쉽
VII_res$z

##             C1           C2
## 1 1.000000e+00 6.786307e-28
## 2 1.000000e+00 8.771316e-27
## 3 1.000000e+00 8.895007e-36
## 4 5.251505e-17 1.000000e+00
## 5 7.046079e-22 1.000000e+00
## 6 1.843399e-26 1.000000e+00
## 7 1.544788e-17 1.000000e+00

# 혼합분포
VII_res$parameters

## $tau
## $tau$C1
## [1] 0.4285714
## 
## $tau$C2
## [1] 0.5714286
## 
## 
## $mu
## $mu$C1
##        x1        x2 
##  5.333333 13.333333 
## 
## $mu$C2
##    x1    x2 
## 11.25  3.50 
## 
## 
## $Sigma
## $Sigma$C1
##          [,1]     [,2]
## [1,] 1.222222 0.000000
## [2,] 0.000000 1.222222
## 
## $Sigma$C2
##         [,1]    [,2]
## [1,] 0.96875 0.00000
## [2,] 0.00000 0.96875

13.5.4 R 패키지 내 모형기반 군집분석

R 패키지 mclust를 통해, 위에서 살펴본 VII, VEI, VEE 외에 보다 다양한 분산-공분산 모형을 가정한 군집분석을 수행할 수 있다 (Scrucca et al. 2016). 다음은 “EEI” 구조에 대한 수행 예이다.

res_mclust_EEI <- mclust::meEEI(df[, -1], z_hat)

위 수행 결과 객체는 리스트 형태이며, 그 원소 중 z는 \(\hat{z}_{ik}\)값을, parameters는 혼합분포 파라미터 추정값 (\(\hat{\tau}_k\), \(\hat{\boldsymbol\mu}_k\), \(\hat{\boldsymbol\Sigma}_k\))을 나타낸다.

res_mclust_EEI$z

##              [,1]         [,2]
## [1,] 6.198742e-26 1.000000e+00
## [2,] 2.193775e-22 1.000000e+00
## [3,] 1.432979e-28 1.000000e+00
## [4,] 1.000000e+00 3.497777e-20
## [5,] 1.000000e+00 1.350932e-26
## [6,] 1.000000e+00 5.217649e-33
## [7,] 1.000000e+00 9.883335e-24

res_mclust_EEI$parameters

## $pro
## [1] 0.5714286 0.4285714
## 
## $mean
##     [,1]      [,2]
## x1 11.25  5.333333
## x2  3.50 13.333333
## 
## $variance
## $variance$modelName
## [1] "EEI"
## 
## $variance$d
## [1] 2
## 
## $variance$G
## [1] 2
## 
## $variance$sigma
## , , 1
## 
##           x1       x2
## x1 0.7738095 0.000000
## x2 0.0000000 1.380952
## 
## , , 2
## 
##           x1       x2
## x1 0.7738095 0.000000
## x2 0.0000000 1.380952
## 
## 
## $variance$Sigma
##           x1       x2
## x1 0.7738095 0.000000
## x2 0.0000000 1.380952
## 
## $variance$scale
## [1] 1.033728
## 
## $variance$shape
## [1] 0.7485618 1.3358950
## 
## 
## $Vinv
## NULL

mclust 패키지 내의 함수 densityMclust는 Bayesian information criterion (BIC)을 기준으로 최적의 혼합분포를 찾는 함수이다. 즉, 내부적으로 여러가지 분산-공분산 모형과 군집 수의 조합에 대한 군집분석을 수행한 뒤, 각 조합의 최종결과에서 얻어진 BIC 값을 기준으로 최적의 조합을 선정한다.

res_mclust_opt <- mclust::densityMclust(df[, -1], verbose = FALSE)

함수 수행결과 객체의 BIC 원소가 나타내는 결과는 아래와 같다.

res_mclust_opt$BIC

## Bayesian Information Criterion (BIC): 
##         EII       VII       EEI       VEI       EVI
## 1 -85.40006 -85.40006 -85.70851 -85.70851 -85.70851
## 2 -62.00992 -63.86240 -63.37677 -65.22485 -65.32204
## 3 -65.47796        NA -66.01911        NA        NA
## 4 -69.04346        NA -70.17240        NA        NA
## 5 -72.02226        NA -73.96817        NA        NA
## 6 -62.27998        NA -64.22589        NA        NA
## 7        NA        NA        NA        NA        NA
##         VVI       EEE       VEE       EVE       VVE
## 1 -85.70851 -75.27433 -75.27433 -75.27433 -75.27433
## 2 -67.17013 -64.66516 -66.60332 -65.06811 -66.92481
## 3        NA -67.87781        NA        NA        NA
## 4        NA -67.31282        NA        NA        NA
## 5        NA        NA        NA        NA        NA
## 6        NA        NA        NA        NA        NA
## 7        NA        NA        NA        NA        NA
##         EEV       VEV       EVV       VVV
## 1 -75.27433 -75.27433 -75.27433 -75.27433
## 2 -65.42506 -67.34154 -66.55375 -68.44666
## 3 -71.48895        NA        NA        NA
## 4        NA        NA        NA        NA
## 5        NA        NA        NA        NA
## 6        NA        NA        NA        NA
## 7        NA        NA        NA        NA
## 
## Top 3 models based on the BIC criterion: 
##     EII,2     EII,6     EEI,2 
## -62.00992 -62.27998 -63.37677

수행 결과 가장 큰 BIC 값을 지닌 최적의 조합은 EII 분산-공분산 모형으로 2개의 군집을 가정했을 때 얻어진다.

densityMclust 함수 수행 결과 얻어진 혼합분포를 plotting해보자.

plot(res_mclust_opt, what = "density",
     data = df[, -1], points.cex = 0.5)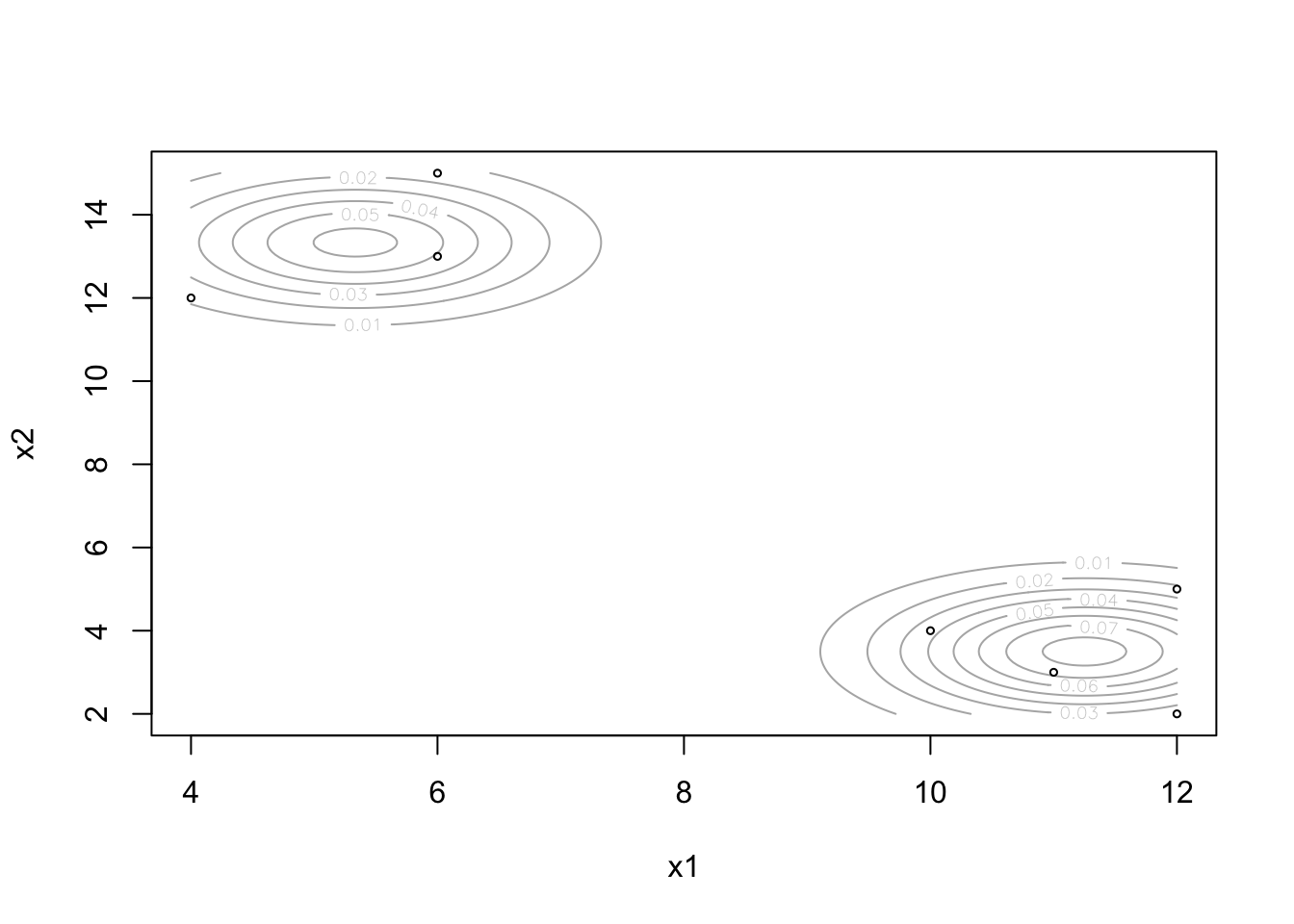

Figure 13.2: mclust::densityMclust 수행 결과 얻어진 혼합분포

References

Banfield, Jeffrey D, and Adrian E Raftery. 1993. “Model-Based Gaussian and Non-Gaussian Clustering.” Biometrics, 803–21.

Celeux, Gilles, and Gérard Govaert. 1995. “Gaussian Parsimonious Clustering Models.” Pattern Recognition 28 (5): 781–93.

Kaufman, L, and P. J. Rousseeuw. 1990. “Finding Groups in Data: An Introduction to Cluster Analysis.”

Park, Hae-Sang, and Chi-Hyuck Jun. 2009. “A Simple and Fast Algorithm for k-Medoids Clustering.” Expert Systems with Applications 36 (2): 3336–41.

Scrucca, Luca, Michael Fop, T Brendan Murphy, and Adrian E Raftery. 2016. “Mclust 5: Clustering, Classification and Density Estimation Using Gaussian Finite Mixture Models.” The R Journal 8 (1): 289.

전치혁. 2012. 데이터마이닝 기법과 응용. 한나래출판사.