Chapter 14 군집해의 평가 및 해석

군집분석 수행 시에는 분류분석과 달리 각 객체가 속하는 군집에 대하여 알려진 학습표본이 없기 때문에 어떤 군집해의 성능을 평가하기가 곤란하다. 각 객체가 이차원 또는 삼차원의 변수로 이루어진 경우에는 각 객체를 좌표축에 나타내어 도식화함으로써 어느 정도 군집해의 타당성을 정성적으로 평가가 가능할 것이나, 이보다 높은 차원의 경우에는 도식화가 불가능하다. 따라서 응용분야에 따라 전문가의 견해가 군집해의 평가에 필요할 수도 있다.

14.1 필요 R package 설치

본 장에서 필요한 R 패키지들은 아래와 같다.

package	version
tidyverse	1.3.1
cluster	2.1.2
flexclust	1.4-0
clValid	0.7

14.2 군집해의 평가

군집해의 정량적인 평가척도에 대한 연구는 지속적으로 이루어지고 있으며, 크게 외부평가지수(external index)와 내부평가지수(internal index)로 구분되고 있다.

14.2.1 외부평가지수

이미 잘 알려진 군집해가 있다고 가정할 때, 새로 제안된 군집해를 기존에 알려진 군집해와 비교하는 평가척도이다.

$n$개의 객체에 대하여 알려진 기준 군집해를 다음과 같다고 하자.

\[\begin{equation*} \mathbf{U} = \{ U_1, U_2, \cdots, U_r \} \end{equation*}\]

즉, 기준 군집해 $\mathbf{U}$는 $r$개의 군집으로 구성되며, $k$번째 군집을 $U_k$로 나타낸다.

유사하게, 비교 대상의 군집해를 다음과 같이 $s$개의 군집으로 구성된 $\mathbf{V}$로 나타내자.

\[\begin{equation*} \mathbf{V} = \{ V_1, V_2, \cdots, V_s \} \end{equation*}\]

14.2.1.1 기본 R 스크립트

다음의 두 군집해 간의 유사도를 랜드지수 및 수정랜드지수를 이용하여 표현할 수 있다.

\[\begin{eqnarray*} U &=& \{ \{1, 2, 3, 4\}, \{5, 6, 7\}, \{8, 9, 10\} \}\\ V &=& \{ \{1, 2, 5, 8\}, \{3, 6, 9\}, \{4, 7, 10\} \} \end{eqnarray*}\]

랜드지수 및 수정랜드지수는 flexclust 패키지의 randIndex 함수를 호출하여 계산할 수 있으며, 랜드지수를 계산할 때는 correct = FALSE, 수정랜드지수를 계산할 때는 correct = TRUE로 파라미터 값을 지정하여야 한다. 파라미터값을 지정하지 않을 때는 기본값으로 수정랜드지수를 계산한다.

sol_1 <- c(1, 1, 1, 1, 2, 2, 2, 3, 3, 3)
sol_2 <- c(1, 1, 2, 3, 1, 2, 3, 1, 2, 3)
map(c(FALSE, TRUE), 
    ~ flexclust::randIndex(x = sol_1, y = sol_2, correct = .x))

## [[1]]
##        RI 
## 0.5111111 
## 
## [[2]]
##   ARI 
## -0.25

14.2.1.2 랜드지수

두 군집해 $U, V$ 내 에서 각 객체가 속한 군집을 나타내기 위한membership 변수를 아래와 같이 정의하자.

\[\begin{equation*} u_{ik} = \begin{cases} 1 & \text{ if object $i$ belongs to cluster $U_k$, i.e. } i \in U_k \\ 0 & \text{ otherwise} \end{cases}, \, i = 1, \cdots, n, \, k = 1, \cdots, r \end{equation*}\]

\[\begin{equation*} v_{ik} = \begin{cases} 1 & \text{ if object $i$ belongs to cluster $V_k$, i.e. } i \in V_k \\ 0 & \text{ otherwise} \end{cases}, \, i = 1, \cdots, n, \, k = 1, \cdots, s \end{equation*}\]

랜드지수를 산출하기 위해, 우선 다음과 같은 네 가지 값을 정의한다.

\[\begin{eqnarray*} a &=& \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} \sum_{k = 1}^{r} \sum_{l = 1}^{s} u_{ik} u_{jk} v_{il} v_{jl}\\ b &=& \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} \sum_{k = 1}^{r} \sum_{l = 1}^{s} u_{ik} u_{jk} v_{il} (1 - v_{jl})\\ c &=& \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} \sum_{k = 1}^{r} \sum_{l = 1}^{s} u_{ik} (1 - u_{jk}) v_{il} v_{jl}\\ d &=& \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} \sum_{k = 1}^{r} \sum_{l = 1}^{s} u_{ik} (1 - u_{jk}) v_{il} (1 - v_{jl}) \end{eqnarray*}\]

이 때, Rand (1971) 가 제안한 랜드지수(Rand index)는 다음과 같이 정의된다.

\[\begin{equation} RI = \frac{a + d}{a + b + c + d} \tag{14.1} \end{equation}\]

여기서, $a + b + c + d$는 객체 쌍의 전체 수를 의미하므로 다음과 같다.

\[\begin{equation*} a + b + c + d = {n \choose 2} \end{equation*}\]

식 (14.1)는 0에서 1 사이의 값을 갖게 되며, 0에 가까울수록 두 군집해가 일치하지 않음을, 1에 가까울수록 두 군집해가 일치함을 나타낸다. 또한 랜드지수는 랜덤하게 작성한 두 군집해 간의 유사도의 기대값이 0보다 크다.

Hubert and Arabie (1985) 는 수정랜드지수(adjusted Rand index)를 아래와 같이 제안하였다.

\[\begin{equation} RI_{adj} = \frac{2 (ad - bc)}{(a + b)(b + d) + (a + c)(c + d)} \tag{14.2} \end{equation}\]

식 (14.2)는 랜덤한 군집해 간의 비교의 경우 0에 가까운 값을 갖는다.

아래 구현한 rand_index 함수는 임의의 두 군집해 u와 v에 대한 랜드지수 및 수정랜드지수를 계산하는 함수이다.

u, v: 서로 비교할 두 개의 군집해 벡터. 각 원소값은 각 객체가 속한 군집을 나타낸다.
다음과 같은 두 개의 component를 지닌 list를 리턴한다.
- ri: 랜드지수
- adj_ri: 수정랜드지수

rand_index <- function(u, v) {
  if (!is_vector(u) || !is_vector(v)) {
    stop("Input needs to be vector")
  } else if (length(u) != length(v)) {
    stop("Vectors u and v must have the same length.")
  }
  
  U <- tibble(
    i = seq_along(u),
    cluster = u
  ) %>%
    inner_join(
      rename(., j = i),
      by = "cluster"
    ) %>%
    select(-cluster) %>%
    filter(i < j) 
  
  V <- tibble(
    i = seq_along(v),
    cluster = v
  ) %>%
    inner_join(
      rename(., j = i),
      by = "cluster"
    ) %>%
    select(-cluster) %>%
    filter(i < j) 
  
  a <- nrow(inner_join(U, V, by = c("i", "j")))
  b <- nrow(anti_join(U, V, by = c("i", "j")))
  c <- nrow(anti_join(V, U, by = c("i", "j")))
  d <- choose(length(u), 2) - (a + b + c)
  
  ri <- (a + d) / (a + b + c + d)
  adj_ri <- 2 * (a * d - b * c) / 
    ((a + b) * (b + d) + (a + c) * (c + d))

  return(list(ri = ri, adj_ri = adj_ri))
}

50개의 객체에 대해 랜덤하게 할당된 군집해(K = 3) 두 개를 비교하여 랜드지수와 수정랜드지수를 구해보자.

random_rand_index <- function(n, r, s) {
  u <- sample.int(r, size = n, replace = TRUE)
  v <- sample.int(s, size = n, replace = TRUE)
  rand_index(u, v)
}

set.seed(500)

rerun(200, random_rand_index(50, 3, 3)) %>%
  bind_rows() %>%
  gather(key = "metric", value = "value") %>%
  ggplot(aes(x = value, fill = metric)) +
  geom_histogram(binwidth = 0.05) +
  scale_x_continuous(limits = c(-1, 1)) +
  scale_fill_discrete(
    name = "index",
    breaks = c("ri", "adj_ri"),
    labels = c("Rand Index", "adjusted Rand Index")
  ) +
  labs(
    title = "Distribution of index values from 200 random assignments",
    x = "index value",
    y = "frequency"
  )

## Warning: Removed 4 rows containing missing values
## (geom_bar).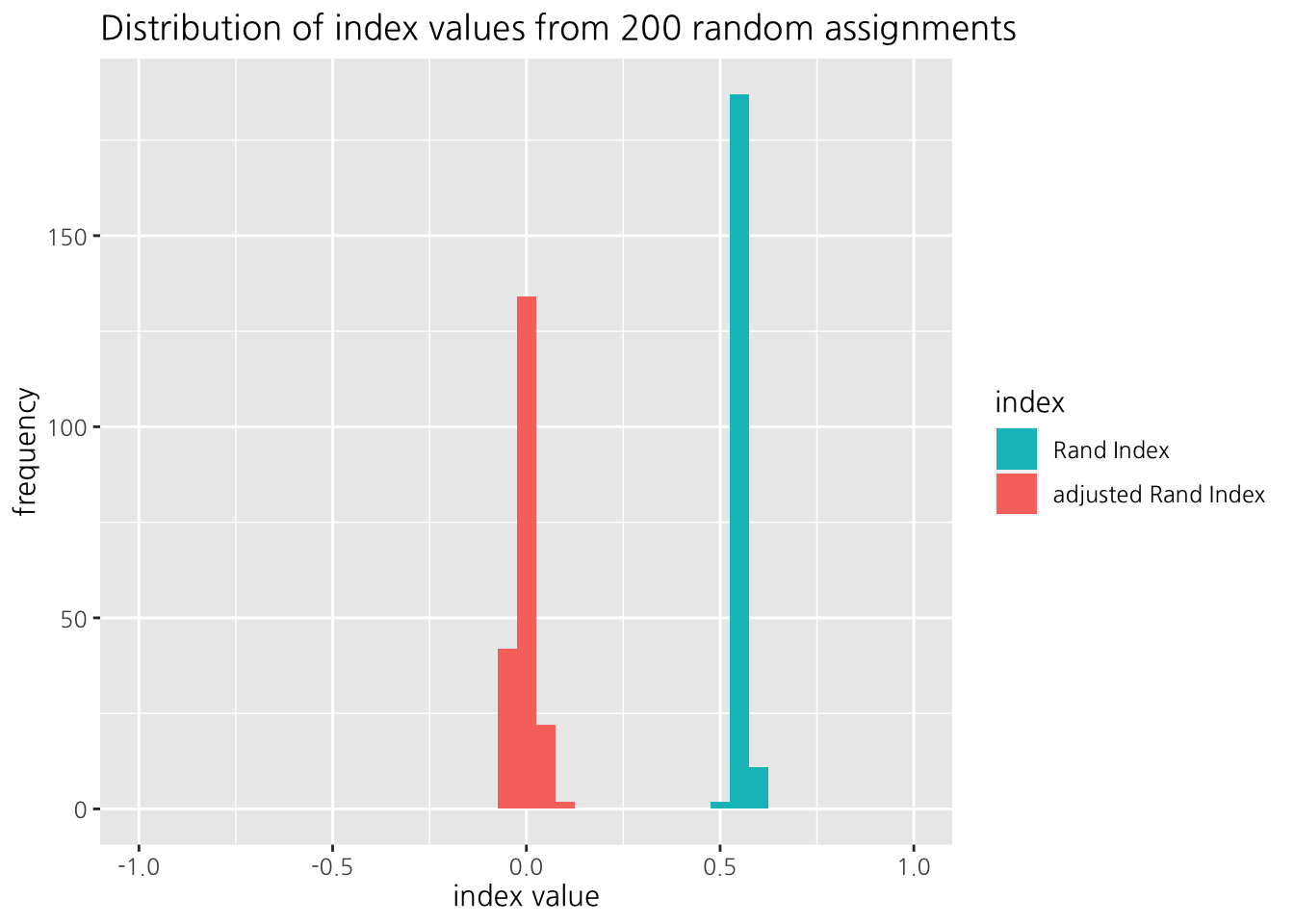

Figure 14.1: 랜덤한 군집해 간 비교: 랜드지수 및 수정랜드지수

Figure 14.1에 보이듯이, 랜덤한 군집해 간 비교에서 랜드지수는 0보다 큰 값을 나타내는 반면, 수정랜드지수는 0을 중심으로 분포되어 있다.

다음의 두 군집해에 대하여 랜드지수와 수정랜드지수를 구해보자.

\[\begin{eqnarray*} U &=& \{(1, 2, 3, 4), (5, 6, 7), (8, 9, 10) \}\\ V &=& \{(1, 2, 5, 8), (3, 6, 9), (4, 7, 10) \} \end{eqnarray*}\]

rand_index(
  c(1, 1, 1, 1, 2, 2, 2, 3, 3, 3),
  c(1, 1, 2, 3, 1, 2, 3, 1, 2, 3)
)

## $ri
## [1] 0.5111111
## 
## $adj_ri
## [1] -0.25

14.2.2 내부평가지수

군집해에 대한 내부평가지수는 외부 정보의 도움 없이 입력 데이터만으로 군집해를 평가하는 척도로써, 주로 밀집성(compactness), 연결성(connectedness), 분리성(spatial separation) 등 세 가지 관점에서 평가한다.

우선 $K$개의 군집으로 이루어진 군집해 $C$가 다음과 같다고 하자.

\[\begin{equation*} C = \{ C_1, C_2, \cdots, C_K \} \end{equation*}\]

14.2.2.1 기본 R 스크립트

아래와 같이 두 개의 변수 $x_1$ 및 $x_2$로 표현되는 객체 데이터에 대해 군집을 찾고자 한다.

df <- tribble(
  ~id, ~x1, ~x2,
  1, 4, 15,
  2, 20, 13,
  3, 3, 13,
  4, 19, 4,
  5, 17, 17,
  6, 8, 11,
  7, 19, 12,
  8, 18, 6
)

df %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r'),
    col.names = c(
      '객체번호', 
      '$x_1$', '$x_2$'
      ),
    caption = '군집 대상 데이터'
  )

Table 14.1: 군집 대상 데이터
객체번호	$x_1$	$x_2$
1	4	15
2	20	13
3	3	13
4	19	4
5	17	17
6	8	11
7	19	12
8	18	6

위 데이터에 대해 다음과 같은 두 개의 다른 군집해를 얻었다고 하자.

\[\begin{equation} \begin{split} U =& \{ \{1, 3, 6\}, \{2, 5, 7\}, \{4, 8\} \}\\ V =& \{ \{1, 3, 6\}, \{2, 4, 5, 7, 8\} \} \end{split} \tag{14.3} \end{equation}\]

sol_1 <- c(1, 2, 1, 3, 2, 1, 2, 3)
sol_2 <- c(1, 2, 1, 2, 2, 1, 2, 2)

본 장에서는 4가지 내부 평가지수를 다룬다. 아래는 R 패키지들에 속한 각각의 함수를 실행하여 그 결과를 리스트 형태로 리턴하는 사용자 정의 함수 cluster_eval를 구현한 것이다. 해당 함수에서 호출하는 R 패키지 함수들은 아래와 같다.

Dunn index (Dunn 1973): clValid::dunn
CH index (Caliński and Harabasz 1974): fpc::calinhara
Connectivity (Handl and Knowles 2005): clValid::connectivity
Silhouettes (Rousseeuw 1987): cluster::silhouette

각각의 평가지수에 대한 자세한 설명은 다음 장에서 하기로 한다.

아래 구현한 사용자 정의함수는 아래와 같은 입력 파라미터를 요구한다.

cluster: 군집 해를 나타내는 길이 $n$, 최대값 $K$의 정수형 벡터
df: 군집 데이터
dist_method: 거리 척도; Dunn, Connectivity, Silhouettes 지수 측정에 사용된다.
nn: 최근 객체 수 (>= 2); Connectivity 측정에 사용된다.

cluster_eval <- function(cluster, df, dist_method = "euclidean", nn = 2) {
  dunn_index <- clValid::dunn(
    Data = df, 
    clusters = cluster, 
    method = dist_method
  )
  
  ch_index <- fpc::calinhara(
    x = df, 
    clustering = cluster
  )
  
  connectivity <- clValid::connectivity(
    Data = df, 
    clusters = cluster, 
    neighbSize = nn
  )
  
  asw <- cluster::silhouette(
    x = cluster, 
    dist = dist(df, method = dist_method)
  )[, "sil_width"] %>% mean()
  
  return(list(
    dunn_index = dunn_index,
    ch_index = ch_index,
    connectivity = connectivity,
    asw = asw
  ))
}

map_dfr(list(sol_1, sol_2), cluster_eval, df = df[, -1], .id = "solution")

## # A tibble: 2 x 5
##   solution dunn_index ch_index connectivity   asw
##   <chr>         <dbl>    <dbl>        <dbl> <dbl>
## 1 1             1.08      26.5            1 0.651
## 2 2             0.822     15.4            0 0.586

14.2.2.2 대표 내부평가지수

Dunn (1973) 은 아래와 같은 지수를 제안하였다.

\[\begin{equation} DI = \frac{\min_{\mathbf{x} \in C_i, \, \mathbf{y} \in C_j \, 1 \leq i \neq j \leq K} d(\mathbf{x}, \mathbf{y})}{\max_{\mathbf{x} \in C_i, \mathbf{y} \in C_i, \, 1 \leq i \leq K} d(\mathbf{x}, \mathbf{y})} \tag{14.4} \end{equation}\]

여기서 분자는 군집 간의 분리성(클수록 분리성이 큼), 분모는 군집의 밀집성(작을수록 밀집성이 높음)을 반영하는 것이라 볼 수 있다. 따라서 분리성과 밀집성이 높을 때 식 (14.4)는 큰 값을 갖게 되며 해당 군집해가 상대적으로 좋게 평가된다.

군집해로부터 식 (14.4)를 계산하는 함수 dunn_index를 아래와 같이 구현해보자. 입력 파라미터는 아래와 같다.

cluster: 각 객체가 속한 군집을 나타내는 길이 $n$의 벡터
df: 객체 데이터를 나타내는 $n$행의 프레임
dist_method: base::dist 함수의 method 파라미터값으로 사용할 거리 척도

dunn_index <- function(cluster, df, dist_method = "euclidean") {
  # 객체 수
  n <- nrow(df)
  
  # 각 객체의 군집해
  cluster_df <- tibble(
    id = 1:n,
    cluster = cluster
  )
  
  # 각 객체 간 거리 데이터 프레임
  # 위 군집해 데이터 프레임과 `inner_join` 을 통해
  # 두 객체가 동일 군집에 속하는지 서로 다른 군집에 속하는 지 표현
  dist_df <- dist(df, method = dist_method, upper = TRUE) %>% 
    broom::tidy() %>%
    mutate_if(is.factor, ~ as.integer(as.character(.))) %>%
    inner_join(
      cluster_df %>% rename(item1 = id, item1_cluster = cluster),
      by = "item1"
      ) %>%
    inner_join(
      cluster_df %>% rename(item2 = id, item2_cluster = cluster),
      by = "item2"
    )
  
  # 서로 다른 군집에 속한 객체 쌍 중
  # 가장 가까운 객체 간의 거리
  numerator <- dist_df %>%
    filter(item1_cluster != item2_cluster) %>%
    top_n(-1, distance) %>%
    slice(1) %>%
    .$distance
  
  # 서로 같은 군집에 속한 객체 쌍 중
  # 가장 먼 객체 간의 거리
  denominator <- dist_df %>%
    filter(item1_cluster == item2_cluster) %>%
    top_n(1, distance) %>%
    slice(1) %>%
    .$distance
  
  res <- numerator / denominator
  
  return(res)
}

map_dbl(list(sol_1, sol_2), dunn_index, df = df[, -1])

## [1] 1.075291 0.822375

Caliński and Harabasz (1974) 는 다음과 같은 지수를 제안하였다.

\[\begin{equation} CH = \frac{\frac{1}{K - 1} \sum_{k = 1}^{K} n_k (\mathbf{c}_k - \mathbf{c})^\top (\mathbf{c}_k - \mathbf{c})}{\frac{1}{n - K} \sum_{k = 1}^{K} \sum_{i \in C_k} (\mathbf{x}_i - \mathbf{c}_k)^\top (\mathbf{x}_i - \mathbf{c}_k)} \tag{14.5} \end{equation}\]

여기에서 $\mathbf{c}_k$는 군집 $k$의 중심좌표(centroid), $\mathbf{c}$는 전체 객체들의 중심좌표, $n_k$는 군집 $C_k$내의 객체 수, $n$은 전체 객체 수를 나타낸다. 식 (14.5) 또한 분자는 분리성, 분모는 밀집성을 평가하며, 값이 클수록 좋은 군집해로 평가된다.

ch_index <- function(cluster, df) {
  # 전체 데이터 중심
  centroid <- df %>% summarize_all(mean)
  
  cluster_df <- df %>% 
    mutate(cluster = cluster) %>%
    group_by(cluster) %>%
    nest()
  
  # 군집 중심
  cluster_centroid_df <- map_dfr(cluster_df$data, ~ summarize_all(., mean))
  
  # 각 군집 중심과 전체 데이터 중심 간 제곱 유클리드 거리
  centroid_dist <- flexclust::dist2(
    cluster_centroid_df, 
    centroid
    )^2
  
  # 각 군집 크기
  cluster_size <- map_dbl(cluster_df$data, nrow)
  
  numerator <- sum(centroid_dist * cluster_size) / (nrow(cluster_df) - 1)
  
  denominator <- map_dbl(
    cluster_df$data,
    # 각 군집 내의 객체와 군집 중심 간 제곱 유클리드 거리의 합
    ~ flexclust::dist2(., summarize_all(., mean))^2 %>% sum()
    ) %>%
    sum() %>%
    `/`(nrow(df) - nrow(cluster_df))

  res <- numerator / denominator
  
  return(res)
}

map_dbl(list(sol_1, sol_2), ch_index, df = df[, -1])

## [1] 26.45029 15.36218

Handl and Knowles (2005) 은 연결성을 반영한 아래와 같은 지수를 제시하고 있다.

\[\begin{equation} Conn = \sum_{i = 1}^{n} \sum_{j = 1}^{L} v_{i, nn_{i}(j)} \tag{14.6} \end{equation}\]

이 때, $nn_{i}(j)$는 객체 $i$의 $j$번째 최근 객체(nearest neighbor)를 나타내며, $L$은 연결성 척도 측정을 위한 사용자 지정 파라미터값이다. 또한 변수 $v_{i, nn_i(j)}$는 아래와 같이 정의된다.

\[\begin{equation*} v_{i, nn_i(j)} = \begin{cases} 0 & \text{ if } \exists C_k : i, nn_i(j) \in C_k \\ 1 / j & \text{ otherwise} \end{cases} \end{equation*}\]

즉, 식 (14.6)는 각 객체가 $j (\leq L)$번째 최근 객체와 다른 객체에 속하면 $1 / j$의 벌점을 부여하는 방식으로, 작은 값일수록 좋은 군집으로 평가될 수 있다.

connectivity <- function(cluster, df, dist_method = "euclidean", n_neighbor = 1) {
  n <- nrow(df)
  
  cluster_df <- tibble(
    id = 1:n,
    cluster = cluster
  )

  # 객체간 거리
  distance_df <- dist(df, method = dist_method, upper = TRUE) %>%
    broom::tidy() %>%
    mutate_if(is.factor, ~ as.integer(as.character(.)))
  
  # 최근 객체
  nn_df <- distance_df %>%
    group_by(item1) %>%
    mutate(nearest = rank(distance, ties.method = "random")) %>%
    filter(nearest <= n_neighbor) %>%
    ungroup() %>%
    inner_join(
      cluster_df %>% rename(item1 = id, item1_cluster = cluster),
      by = "item1"
      ) %>%
    inner_join(
      cluster_df %>% rename(item2 = id, item2_cluster = cluster),
      by = "item2"
    )
  
  # 연결성 계산
  nn_df %>%
    filter(item1_cluster != item2_cluster) %>%
    mutate(v = 1 / nearest) %>%
    .$v %>%
    sum()
  
}

map_dbl(list(sol_1, sol_2), connectivity, df = df[, -1], n_neighbor = 1)

## [1] 0 0

map_dbl(list(sol_1, sol_2), connectivity, df = df[, -1], n_neighbor = 2)

## [1] 1 0

Rousseeuw (1987) 은 실루엣(silhouettes)이라는 내부평가지수를 제안하였다. 우선 다음과 같은 기호를 정의하자.

$a(i)$: 객체 $i$와 동일 군집에 속한 다른 객체들과의 평균 거리
$d(i, C_k)$: 객체 $i$와 다른 군집 $C_k$에 속한 모든 객체들과의 평균 거리, $i \notin C_k$
$b(i) = \min_{k: i \notin C_k} d(i, C_k)$

객체의 군집 멤버쉽 변수 $z_{ik}$를

\[\begin{equation*} z_{ik} = \begin{cases} 1 & \text{ if } i \in C_k\\ 0 & \text{ otherwise } \end{cases} \end{equation*}\]

라 정의하면, 위 $a(i)$와 $b(i)$를 아래와 같이 수식화할 수 있다.

\[\begin{eqnarray*} a(i) &=& \sum_{k = 1}^{K} z_{ik} \frac{\sum_{j \neq i} z_{jk} d(\mathbf{x}_i, \mathbf{x}_j)}{\sum_{j \neq i} z_{jk}}\\ b(i) &=& \max_{k: z_{ik} \neq 1} \frac{\sum_{j \neq i} z_{jk} d(\mathbf{x}_i, \mathbf{x}_j)}{\sum_{j \neq i} z_{jk}} \end{eqnarray*}\]

이 때 객체 $i$에 대한 실루엣은 아래와 같이 정의된다.

\[\begin{equation} s(i) = \frac{b(i) - a(i)}{\max \{ a(i), b(i) \}} \tag{14.7} \end{equation}\]

식 (14.7)은 -1과 1 사이의 값을 갖는데, 1에 가까울수록 객체 $i$가 비슷한 객체들과 군집된 것으로, -1에 가까울수록 먼 객체들과 군집된 것으로 판단할 수 있다.

객체 $i$가 어떠한 다른 객체와도 같은 군집에 속하지 않는 경우가 발생할 수 있다 ($i \in C_k, \, \left| C_k \right| = 1$). 이 경우 $a(i)$가 정의되지 않으므로 $s(i)$값이 식 (14.7)에 의해서 정의되지 않는다. 이러한 경우에는 $s(i) = 0$이라고 실루엣을 정의한다.

\[\begin{equation} s(i) = \begin{cases} \frac{b(i) - a(i)}{\max \{ a(i), b(i) \}} & \text{ if $a(i)$ is defined}\\ 0 & \text{ otherwise } \end{cases} \tag{14.8} \end{equation}\]

이후 군집해의 평가지표로써 평균실루엣(overall average silhouette width; ASW)을 다음과 같이 정의하여 사용한다.

\[\begin{equation} ASW = \frac{1}{n} \sum_{i = 1}^{n} s(i) \tag{14.9} \end{equation}\]

asw <- function(cluster, df, dist_method = "euclidean") {
  n <- nrow(df)
  
  cluster_df <- tibble(
    id = 1:n,
    cluster = cluster
  )
  
  dist_df <- dist(df, method = dist_method, upper = TRUE) %>% 
    broom::tidy() %>%
    mutate_if(is.factor, ~ as.integer(as.character(.))) %>%
    inner_join(
      cluster_df %>% rename(item1 = id, item1_cluster = cluster),
      by = "item1"
      ) %>%
    inner_join(
      cluster_df %>% rename(item2 = id, item2_cluster = cluster),
      by = "item2"
    )
  
  dist_df <- dist_df %>%
    group_by(item1, item1_cluster, item2_cluster) %>%
    summarize(
      avg_distance = mean(distance)
    )
  
  a <- dist_df %>%
    filter(item1_cluster == item2_cluster) %>%
    .$avg_distance
  
  b <- dist_df %>%
    filter(item1_cluster != item2_cluster) %>%
    top_n(-1, avg_distance) %>%
    slice(1) %>%
    .$avg_distance
  
  s <- map2_dbl(a, b, ~ (.y - .x) / max(.x, .y))
  
  mean(s)
}

map_dbl(list(sol_1, sol_2), asw, df = df[, -1], dist_method = "euclidean")

## `summarise()` has grouped output by 'item1', 'item1_cluster'. You can override using the `.groups` argument.
## `summarise()` has grouped output by 'item1', 'item1_cluster'. You can override using the `.groups` argument.

## [1] 0.6507364 0.5864226

14.3 군집해의 해석

군집분석의 주목적을 달성하기 위해서는 군집해를 얻은 후 이에 대한 해석이 가능하여야 할 것이다. 즉, 각 군집의 특성을 파악할 수 있어야 실제 문제에 적용할 수 있을 것이다. 이를 위해서는 특정 응용분야의 전문가 지식을 요하는 경우가 많다. 그러나 첫 출발은 각 군집의 중심좌표, 즉 군집 별 변수별 평균치를 산출하는 것이다. 대부분의 경우 변수별 평균치로 군집들을 비교함으로써 군집의 특성을 파악할 수 있다. 다변량을 처리할 수 있는 그래프 역시 도움이 되며, 특히 다변량인 경우 요인분석(factor analysis)를 활용하기도 한다. 최종적으로 각 군집에 대한 특성이 파악되면 명명(naming)하는 것이 추천된다.

References

Caliński, Tadeusz, and Jerzy Harabasz. 1974. “A Dendrite Method for Cluster Analysis.” Communications in Statistics 3 (1): 1–27.

Dunn, Joseph C. 1973. “A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters.”

Handl, Julia, and Joshua Knowles. 2005. “Exploiting the Trade-Off—the Benefits of Multiple Objectives in Data Clustering.” In International Conference on Evolutionary Multi-Criterion Optimization, 547–60. Springer.

Hubert, Lawrence, and Phipps Arabie. 1985. “Comparing Partitions.” Journal of Classification 2 (1): 193–218.

Rand, William M. 1971. “Objective Criteria for the Evaluation of Clustering Methods.” Journal of the American Statistical Association 66 (336): 846–50.

Rousseeuw, Peter J. 1987. “Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis.” Journal of Computational and Applied Mathematics 20: 53–65.

Table 14.1: 군집 대상 데이터
객체번호	\(x_1\)	\(x_2\)
1	4	15
2	20	13
3	3	13
4	19	4
5	17	17
6	8	11
7	19	12
8	18	6