Chapter 12 계층적 군집방법

계층적 군집방법에는 집괴법과 분리법이 있으나 주로 집괴법이 사용된다. 본 장에서는 집괴법으로는 연결법을 소개하고, 분리법으로는 다이아나(DIANA)를 소개한다.

12.1 필요 R 패키지 설치

본 장에서 필요한 R 패키지들은 아래와 같다.

package version
tidyverse 1.3.1
stats 4.1.3
cluster 2.1.2

12.2 군집 간 거리척도 및 연결법

계층적 군집방법에서는 유사한 객체들을 군집으로 묶고, 다시 유사한 군집을 새로운 군집으로 묶는 등 단계적 절차를 사용한다. 이를 위해서는 군집 간의 유사성 척도 혹은 비유사성 척도가 필요하다.

  • \(C_i\): \(i\)번째 군집(군집 \(i\))
  • \(|C_i|\): 군집 \(i\)의 객체수
  • \(\mathbf{c}_i = \left( \bar{x}_1^{(i)}, \bar{x}_2^{(i)}, \cdots, \bar{x}_p^{(i)} \right)\): 군집 \(i\)의 중심좌표(centroid) (\(\bar{x}_a^{(i)} = \frac{1}{|C_i|} \sum_{j \in C_i} x_{aj}\))
  • \(d(u, v) = d(\mathbf{x}_u, \mathbf{x}_v)\): 객체 \(u\)와 객체 \(v\)의 거리(또는 비유사성 척도)
  • \(D(C_i, C_j)\): 군집 \(i\)와 군집 \(j\)의 거리(또는 비유사성 척도)

군집과 군집 간의 거리척도를 평가하는 방법에 따라 다양한 연결법(linkage method)이 존재한다. 아래에 대표적인 연결법과 군집 간 거리척도를 소개한다.

Table 12.1: 연결법 종류
연결법 군집거리 \(D(C_i, C_j)\)
단일연결법(single linkage method) \(\min_{u \in C_i, \, v \in C_j} d(u, v)\)
완전연결법(complete linkage method) \(\max_{u \in C_i, \, v \in C_j} d(u, v)\)
평균연결법(average linkage method) \(\frac{1}{\lvert C_i \rvert \lvert C_j \rvert} \sum_{u \in C_i, \, v \in C_j} d(u, v)\)
중심연결법(centroid linkage method) \(d(\mathbf{c}_i, \mathbf{c}_j)\)

12.3 연결법의 군집 알고리즘

12.3.1 기본 R 스크립트

train_df <- tibble(
  id = c(1:10),
  x1 = c(6, 8, 14, 11, 15, 7, 13, 5, 3, 3),
  x2 = c(14,13, 6, 8, 7, 15, 6, 4, 3, 2)
)

knitr::kable(train_df, booktabs = TRUE,
             align = c('r', 'r', 'r'),
             col.names = c('객체번호', 'PC 경력(년, $x_1$)', '사용시간(시간, $x_2$)'),
             caption = 'PC 사용자 데이터')
Table 12.2: PC 사용자 데이터
객체번호 PC 경력(년, \(x_1\)) 사용시간(시간, \(x_2\))
1 6 14
2 8 13
3 14 6
4 11 8
5 15 7
6 7 15
7 13 6
8 5 4
9 3 3
10 3 2 
theme_set(theme_gray(base_family='NanumGothic'))
ggplot(train_df, aes(x = x1, y = x2)) +
  geom_text(aes(label = id)) +
  xlab("PC 경력") +
  ylab("사용시간")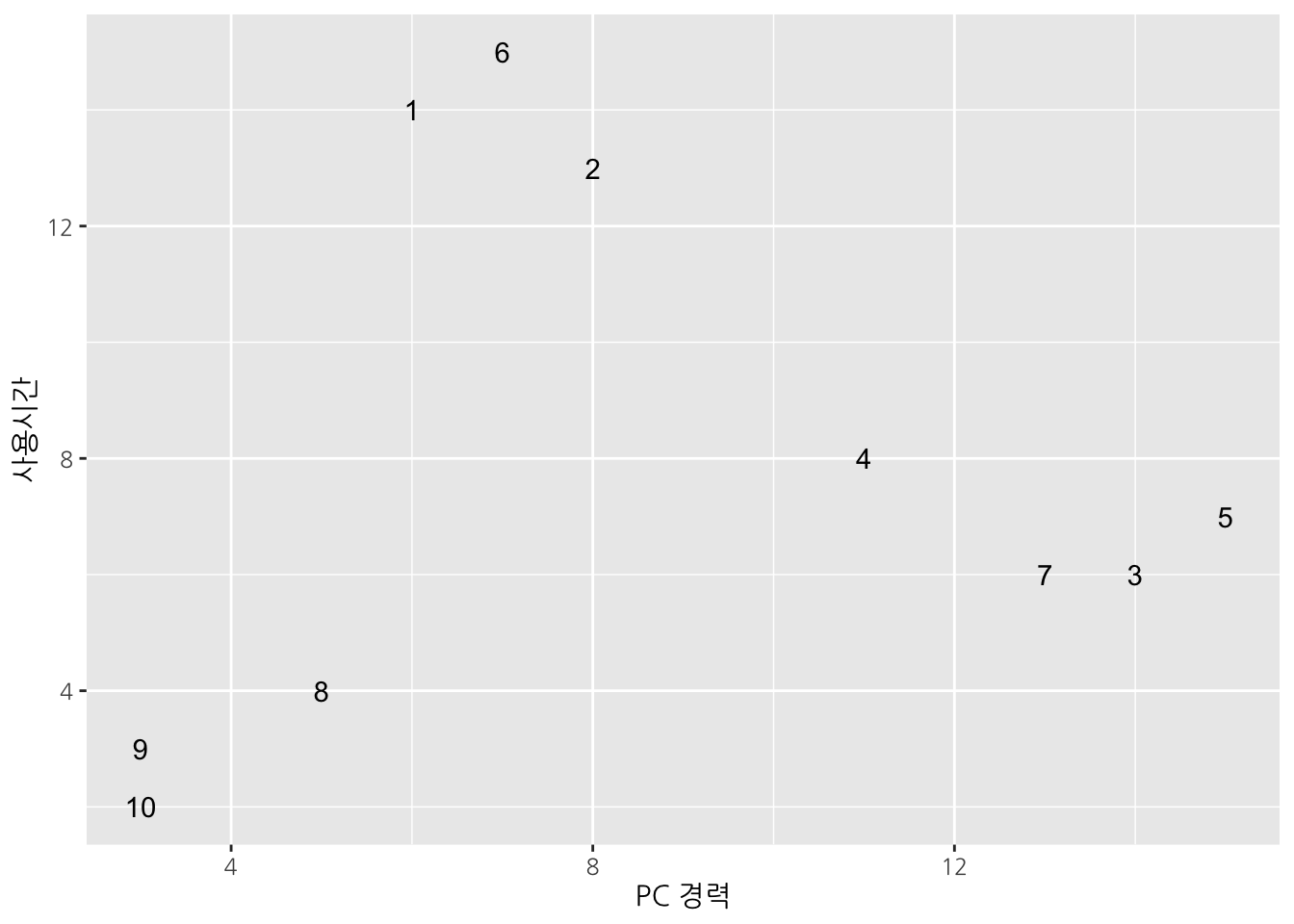
PC 사용자 데이터

Figure 12.1: PC 사용자 데이터

Table 12.2는 10명의 사람(객체)에 대한 PC 사용경력과 주당 PC 사용시간을 나타낸 것이다. 각 객체가 두 변수로 이루어져 있으며, Figure 12.1에서 보는 바와 같이 세 개의 군집({1, 2, 6}, {3, 4, 5, 7}, {8, 9, 10})으로 이루어져 있다고 볼 수 있다.

본 장에서 평균연결법에 의한 군집화 과정을 살펴보기로 하자. 우선 R 패키지를 이용해서 간단하게 군집해를 구하는 과정은 아래와 같다.

  1. stats 패키지의 함수 dist를 이용하여 객체간 거리를 계산한다.
  2. 1에서 얻은 거리 행렬을 stats 패키지의 hclust 함수에 입력하여 데이터 군집을 분석한다. 이 때, 파라미터 method의 값을 “average”로 설정하면 평균연결법을 이용한다.
dist(train_df[, -1]) %>%
  hclust(method = "average") %>%
  plot(
    main = NULL,
    ylab = "distance",
    xlab = "observation"
  )
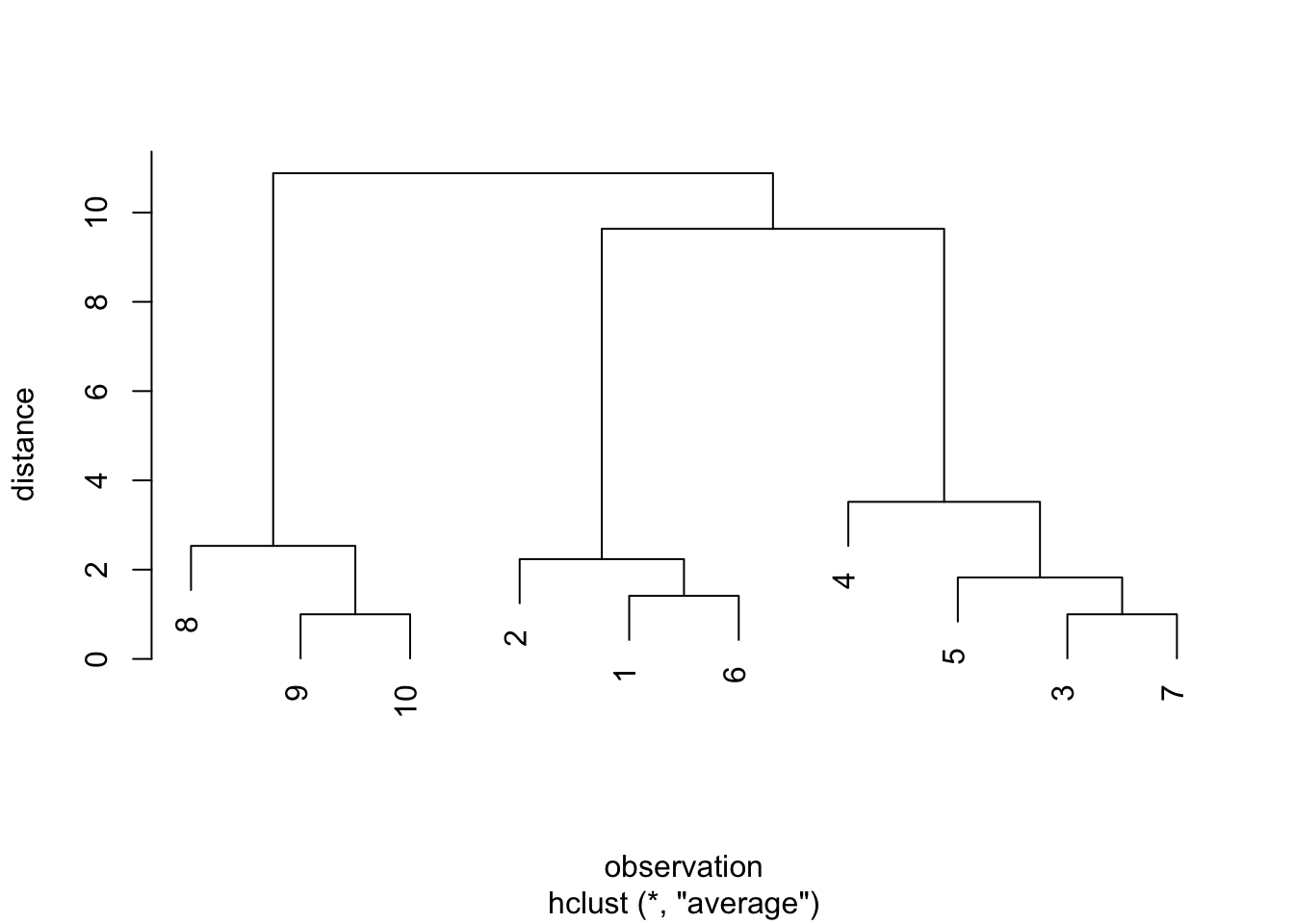
PC 사용자 데이터에 대한 평균연결법 덴드로그램

Figure 12.2: PC 사용자 데이터에 대한 평균연결법 덴드로그램

12.3.2 연결법 군집 알고리즘

각 연결법들은 군집간 유사성 척도 평가 방법이 다를 뿐, 군집화를 위한 알고리즘은 동일하게 아래와 같이 진행된다.

  1. 단계0: 초기화
    1. 연결법을 선정한다.
    2. 각 객체를 하나의 군집으로 간주한다.
    3. \(k \leftarrow n\)
  2. 단계1: 군집
    1. 현재의 군집결과에 있는 모든 군집 간의 쌍에 대하여 \(D(C_i, C_j)\)를 산출하여, 이 중 최소가 되는 군집 \(i\)와 \(j\)를 묶어 하나의 군집으로 만든 후 군집결과를 수정한다.
    2. \(k \leftarrow k - 1\)
  3. 단계2: \(k = 1\)이면 Stop, 그렇지 않으면 단계 1을 반복한다.

단계1은 객체 수 \(n\)만큼 반복된다.

iteration <- vector("list", length = nrow(train_df))

임의의 군집해에 대하여, 단계1을 수행하는 함수를 아래와 같이 구현해보자. 아래 함수 merge_cluster는 아래와 같은 두 개의 입력변수를 사용한다.

  • df: 객체 데이터 프레임. 열 이름이 id인 열은 객체번호를 나타내어, 객체간 거리 계산에 포함하지 않는다.
  • cluster_label: 두 개의 열로 이루어진 데이터 프레임. 열 id는 객체번호를 나타내며, 열 cluster는 군집 이름을 나타낸다. 하나의 객체는 하나의 군집에만 속할 수 있으나, 하나의 군집은 여러 개의 객체를 포함할 수 있다.

함수 수행 결과, 아래와 같은 세 개의 원소를 지닌 리스트를 리턴한다.

  • cluster_dist: 군집 간 거리를 나타낸 데이터 프레임. 평균연결법에 기반한 거리.
  • closest_clusters: 입력된 군집해 내에서 가장 가까운 두 군집을 나타낸 데이터 프레임. 두 열 item1과 item2는 각각 군집 이름을 나타내며, distance는 해당 두 군집간의 거리를 나타낸다.
  • new_cluster_label: closest_clusters에 포함된 두 군집을 하나로 묶어 새로운 군집을 만든 후 얻어진 군집해.
merge_cluster <- function(df, cluster_label) {
  # 군집간 거리 계산한다. - 유클리드 거리 및 평균연결법 기반
  cluster_dist <- dist(subset(df, select = -id), upper = TRUE) %>% 
    broom::tidy() %>%
    mutate_if(is.factor, ~ as.integer(as.character(.))) %>%
    inner_join(
      cluster_label %>% rename(
        item1 = id, cluster1 = cluster
        ),
      by = "item1") %>%
    inner_join(
      cluster_label %>% rename(
        item2 = id, cluster2 = cluster
        ),
      by = "item2") %>%
    filter(cluster1 != cluster2) %>%
    group_by(cluster1, cluster2) %>%
    summarize(distance = mean(distance)) %>%
    ungroup()
  
  # 서로 가장 가깝게 위치하는 두 군집을 찾는다.
  closest_clusters <- cluster_dist %>%
    arrange(distance) %>%
    slice(1)
  
  # 군집해를 업데이트한다.
  cluster_label[
    cluster_label$cluster %in% (
      closest_clusters[, c("cluster1", "cluster2")] %>% unlist()
    ),
    "cluster"
  ] <- paste(
    closest_clusters[, c("cluster1", "cluster2")] %>% unlist(),
    collapse = ","
    )
  
  list(cluster_dist = cluster_dist, 
       closest_clusters = closest_clusters, 
       new_cluster_label = cluster_label)
}

우선 단계 0에서 얻어지는 군집해에 대한 데이터를 아래와 같이 생성한다.

init_cluster <- tibble(
  id = train_df$id,
  cluster = as.character(1:nrow(train_df))
)

print(unique(init_cluster$cluster))
##  [1] "1"  "2"  "3"  "4"  "5"  "6"  "7"  "8"  "9"  "10"
k <- length(unique(init_cluster$cluster))

print(k)
## [1] 10

위와 같이, 초기 군집해에서 군집 수는 전체 객체수와 같은 10개이다.

위 초기해로부터 단계1을 아래와 같이 수행해보자.

iteration[[1]] <- merge_cluster(train_df, init_cluster)
## `summarise()` has grouped output by 'cluster1'. You can override using the `.groups` argument.

찾아진 가장 가까운 두 군집은 아래와 같다.

iteration[[1]]$closest_cluster
## # A tibble: 1 x 3
##   cluster1 cluster2 distance
##   <chr>    <chr>       <dbl>
## 1 10       9               1

위 두 군집을 하나로 묶은 새로운 군집해는 아래와 같다.

iteration[[1]]$new_cluster_label
## # A tibble: 10 x 2
##       id cluster
##    <int> <chr>  
##  1     1 1      
##  2     2 2      
##  3     3 3      
##  4     4 4      
##  5     5 5      
##  6     6 6      
##  7     7 7      
##  8     8 8      
##  9     9 10,9   
## 10    10 10,9

위 새로운 군집해의 군집 수는 9이다. 이는 아직 1보다 크므로, 새로 얻어진 군집해로부터 단계 1을 반복한다.

iteration[[2]] <- merge_cluster(
  train_df,
  iteration[[1]]$new_cluster_label
)
## `summarise()` has grouped output by 'cluster1'. You can override using the `.groups` argument.

이번에 찾아진 가장 가까운 두 군집은 아래와 같다.

iteration[[2]]$closest_cluster
## # A tibble: 1 x 3
##   cluster1 cluster2 distance
##   <chr>    <chr>       <dbl>
## 1 3        7               1

위 두 군집을 하나로 묶은 새로운 군집해는 아래와 같다.

iteration[[2]]$new_cluster_label
## # A tibble: 10 x 2
##       id cluster
##    <int> <chr>  
##  1     1 1      
##  2     2 2      
##  3     3 3,7    
##  4     4 4      
##  5     5 5      
##  6     6 6      
##  7     7 3,7    
##  8     8 8      
##  9     9 10,9   
## 10    10 10,9

위 군집해에 기반하여 단계 1을 다시 반복해보자.

iteration[[3]] <- merge_cluster(
  train_df,
  iteration[[2]]$new_cluster_label
)
## `summarise()` has grouped output by 'cluster1'. You can override using the `.groups` argument.
print(iteration[[3]]$closest_cluster)
## # A tibble: 1 x 3
##   cluster1 cluster2 distance
##   <chr>    <chr>       <dbl>
## 1 1        6            1.41
print(iteration[[3]]$new_cluster_label)
## # A tibble: 10 x 2
##       id cluster
##    <int> <chr>  
##  1     1 1,6    
##  2     2 2      
##  3     3 3,7    
##  4     4 4      
##  5     5 5      
##  6     6 1,6    
##  7     7 3,7    
##  8     8 8      
##  9     9 10,9   
## 10    10 10,9

위와 같은 과정을 전체 객체가 하나의 군집으로 묶일 때까지 아래와 같이 반복하며 군집결과를 출력해보자.

#단계0
init_cluster <- tibble(
  id = train_df$id,
  cluster = as.character(1:nrow(train_df))
)

i <- 0L
current_clusters <- unique(init_cluster$cluster)
k <- length(current_clusters)

print_clusters <- function(i, k, clusters) {
  cat("Iteration: ", i, ", k = ", k, ", clusters = ", paste0("{", clusters, "}"), "\n")
}

print_clusters(i, k, current_clusters)
## Iteration:  0 , k =  10 , clusters =  {1} {2} {3} {4} {5} {6} {7} {8} {9} {10}
#단계1
iteration <- vector("list", length = nrow(train_df) - 1)
while(k > 1) {
  i <- i + 1
  if(i == 1) {
    iteration[[i]] <- merge_cluster(
      train_df,
      init_cluster
    )
  } else {
    iteration[[i]] <- merge_cluster(
      train_df,
      iteration[[i-1]]$new_cluster_label
    )
  }

  current_clusters <- unique(iteration[[i]]$new_cluster_label$cluster)
  k <- length(current_clusters)
  
  print_clusters(i, k, current_clusters)
}
## Iteration:  1 , k =  9 , clusters =  {1} {2} {3} {4} {5} {6} {7} {8} {10,9} 
## Iteration:  2 , k =  8 , clusters =  {1} {2} {3,7} {4} {5} {6} {8} {10,9} 
## Iteration:  3 , k =  7 , clusters =  {1,6} {2} {3,7} {4} {5} {8} {10,9} 
## Iteration:  4 , k =  6 , clusters =  {1,6} {2} {3,7,5} {4} {8} {10,9} 
## Iteration:  5 , k =  5 , clusters =  {1,6,2} {3,7,5} {4} {8} {10,9} 
## Iteration:  6 , k =  4 , clusters =  {1,6,2} {3,7,5} {4} {10,9,8} 
## Iteration:  7 , k =  3 , clusters =  {1,6,2} {3,7,5,4} {10,9,8} 
## Iteration:  8 , k =  2 , clusters =  {1,6,2,3,7,5,4} {10,9,8} 
## Iteration:  9 , k =  1 , clusters =  {1,6,2,3,7,5,4,10,9,8}

12.3.3 R 패키지 내 연결법

R에서는 stats 패키지의 hclust 함수를 이용하여 군집해를 구할 수 있다.

우선, 객체간 거리 행렬을 함수 dist를 이용하여 구한다. 아래는 유클리드 거리를 구하는 예이며, 상황에 따라 다른 거리 척도를 이용할 수도 있다.

distance_matrix <- dist(train_df[, -1])

객체간 거리를 구한 후, 함수 hclust를 이용하여 군집분석을 수행한다. 기본설정은 완전연결법이며, 파라미터 method의 값을 설정함으로써 단일연결법, 평균연결법, 중심연결법을 수행할 수 있다.

cluster_solution <- hclust(distance_matrix, method = "average")

결과 객체 cluster_solution는 아래와 같은 컴포넌트(components)를 지닌 리스트(list) 객체이다.

names(cluster_solution)
## [1] "merge"       "height"      "order"      
## [4] "labels"      "method"      "call"       
## [7] "dist.method"

이 중, merge는 2개의 열과 \(n - 1\)개의 행으로 이루어진 행렬로, 연결법 알고리즘의 단계1 iteration에서 묶어지는 두 군집을 기록한 것이다.

cluster_solution$merge
##       [,1] [,2]
##  [1,]   -3   -7
##  [2,]   -9  -10
##  [3,]   -1   -6
##  [4,]   -5    1
##  [5,]   -2    3
##  [6,]   -8    2
##  [7,]   -4    4
##  [8,]    5    7
##  [9,]    6    8

위에서 각 행은 iteration을 나타내며, 두 열은 묶어지는 두 군집을 나타낸다. 값이 0보다 작은 경우에는 번호가 원 객체 번호를 나타내며, 값이 0보다 큰 경우에는 해당 번호의 iteration에서 묶어진 군집을 나타낸다. 예를 들어, 위 결과의 6번째 행 (-8, 2) 은 객체 8과 두 번째 iteration에서 얻어진 군집 (객체 9와 10이 묶여진 군집)이 묶여 하나의 군집(객체 8, 9, 10)을 이루게 됨을 나타낸다.

height는 각 iteration에서 묶이는 두 군집간의 거리를 나타내며, 위 Figure 12.2의 덴드로그램에서 세로선의 높이를 나타낸다. Iteration이 증가함에 따라 묶이는 두 군집간의 거리도 증가한다. 일반적으로 이 거리값이 크게 증가하는 iteration에서 두 군집을 묶지 않고 최종 군집해를 도출한다.

cluster_solution$height
## [1]  1.000000  1.000000  1.414214  1.825141  2.236068
## [6]  2.532248  3.519028  9.635217 10.881878

위 결과의 경우 iteration 8에서 거리값이 크게 증가한다. 이는 위 Figure 12.2의 덴드로그램에서 3개의 군집에서 2개의 군집으로 묶이는 과정에서 세로선의 높이가 현격히 증가하는 지점이다. 따라서, iteration 7에서 얻어진 3개의 군집이 적절한 군집해라 판단할 수 있겠다.

12.4 워드 방법

워드방법(Ward’s method) 역시 각 객체를 하나의 군집으로 간주함을 시작으로 군집들을 묶어 단계적으로 그 수를 하나가 돌 때까지 줄여나가는 것인데, 군집의 제곱합을 활용한다.

12.4.1 기본 R 스크립트

아래 Table 12.3는 8명의 운전자에 대한 운전경력과 교통위반 횟수를 나타낸 것이다.

train_df <- tibble(
  id = c(1:8),
  x1 = c(4, 20, 3, 19, 17, 8, 19, 18),
  x2 = c(15, 13, 13, 4, 17, 11, 12, 6)
)

knitr::kable(train_df, booktabs = TRUE,
             align = c('r', 'r', 'r'),
             col.names = c('객체번호', '운전경력($x_1$)', '위반횟수($x_2$)'),
             caption = '운전경력에 따른 교통위반 횟수')
Table 12.3: 운전경력에 따른 교통위반 횟수
객체번호 운전경력(\(x_1\)) 위반횟수(\(x_2\))
1 4 15
2 20 13
3 3 13
4 19 4
5 17 17
6 8 11
7 19 12
8 18 6

앞 절의 연결법에서 사용했던 hclust 함수를 이용하여 워드 방법에 의한 군집해도 구할 수 있으며, 이 때 파라미터 method의 값으로 “ward.D2”를 사용한다.

dist(train_df[, -1]) %>%
  hclust(method = "ward.D2") %>%
  plot(
    main = NULL,
    xlab = "observation"
  )
운전자 데이터에 대한 워드 방법 덴드로그램

Figure 12.3: 운전자 데이터에 대한 워드 방법 덴드로그램

12.4.2 워드 군집 알고리즘

군집결과가 \(\mathbf{C} = \{ C_1, C_2, \cdots, C_k \}\)일 때, 군집 \(C_i\) 내의 제곱합(within sum of squares)은 다음과 같이 산출된다.

\[\begin{equation*} SS(C_i) = \sum_{u \in C_i} \left(\mathbf{x}_u - \mathbf{c}_i\right)^\top\left(\mathbf{x}_u - \mathbf{c}_i\right) \end{equation*}\]

이 때, 전체 군집 내 제곱합을 \(SSW\)라 할 때, 이는 다음과 같다.

\[\begin{equation*} SSW = \sum_{i = 1}^{k} SS(C_i) \end{equation*}\]

다음으로, 현 군집의 각 쌍을 묶는다고 할 때의 새로운 \(SSW\)를 산출한 후, 이 값이 가장 작게 되는 군집 쌍을 묶는다.

  1. 단계0
    1. 각 객체를 하나의 군집으로 간주한다.
    2. \(k \leftarrow n\)
  2. 단계1
    1. 현재의 군집 결과에 있는 모든 군집간의 쌍에 대하여 묶을 경우 전체제곱합(SSW)을 산출하고, 이 중 최소가 되는 군집 \(i\)와 군집 \(j\)를 묶어 하나의 군집으로 만든 후, 군집 결과를 수정한다.
    2. \(k \leftarrow k - 1\)
  3. 단계2: \(k = 1\)이면 Stop, 그렇지 않으면 단계1을 반복한다.

워드 군집 알고리즘을 R script로 구현해보자. 우선, 객체 데이터 \(SSW\)를 계산하는 사용자 정의 함수 calculate_ssw를 아래와 같이 두 입력변수 df 및 cluster_label를 이용하여 구현하자.

  • df: 객체 데이터 프레임. 열 이름이 id인 열은 객체번호를 나타내어, 객체간 거리 계산에 포함하지 않는다.
  • cluster_label: 두 개의 열로 이루어진 데이터 프레임. 열 id는 객체번호를 나타내며, 열 cluster는 군집 이름을 나타낸다. 하나의 객체는 하나의 군집에만 속할 수 있으나, 하나의 군집은 여러 개의 객체를 포함할 수 있다.
# SSW 계산
calculate_ssw <- function(df, cluster_label) {
  df %>%
    inner_join(cluster_label, by = "id") %>%
    group_by(cluster) %>%
    select(-id) %>%
    summarize_all(function(x) sum((x - mean(x))^2)) %>%
    ungroup() %>%
    mutate(ss = rowSums(subset(., select = -cluster))) %>%
    `[[`("ss") %>%
    sum()
}

워드 군집 알고리즘은 현재 군집해 내의 모든 군집쌍에 대하여 두 군집을 하나의 군집으로 묶을 경우의 \(SSW\)를 계산해야 한다. 따라서, 우선 고려할 모든 군집해를 생성하는 사용자 정의 함수 generate_clusters를 아래와 같이 구현한다.

아래 사용자 정의 함수 generate_clusters는 임의의 군집해 cluster_label을 입력변수로 사용하며, 해당 입력변수에 대한 설명은 위 함수 calculate_ssw에서와 같다. 함수 수행 결과, 가능한 각각의 군집쌍 결합의 결과물인 군집해 데이터 프레임을 리스트(list) 형태로 출력한다.

# 임의의 군집해로부터 가능한 다음단계 군집해 생성
generate_clusters <- function(cluster_label) {
  unique_clusters <- unique(cluster_label$cluster)
  
  potential_pairs <- crossing(cluster1 = unique_clusters, 
           cluster2 = unique_clusters) %>%
    filter(cluster1 < cluster2) %>%
    mutate(cluster = paste(cluster1, cluster2, sep = ","))
  
  candidate_solutions <- potential_pairs %>%
    rowwise() %>%
    do(candidate_solution = merge_cluster(cluster_label, .)) %>%
    `[[`("candidate_solution")
  
  candidate_solutions
}

위에서 보이는 바와 같이, 함수 generate_clusters는 또 다른 사용자 정의함수 merge_cluster를 호출한다. 이 함수는 두 입력변수 cluster_label 및 cluster_merge를 사용하는데, cluster_label에 대한 설명은 위 다른 사용자 정의 함수에서와 동일하며, cluster_merge에 대한 설명은 아래와 같다.

  • cluster_merge: 3차원 character 벡터. 첫 두 element는 현재 cluster_label에 존재하는 군집 중 하나의 군집으로 묶일 두 군집의 이름을 나타내며, 세 번째 element는 그 결과 나타나는 군집 이름을 나타낸다.

함수 수행 결과, 입력된 cluster_label에서 군집이름이 cluster_merge[1] 혹은 cluster_merge[2]에 해당하는 객체들은, 출력된 군집해에서는 군집이름 cluster_merge[3]을 지닌다.

# 임의의 군집 결합 규칙 cluster_merge에 따른 군집해
merge_cluster <- function(cluster_label, cluster_merge) {
  idx <- cluster_label$cluster %in% cluster_merge[1:2]
  cluster_label[idx, "cluster"] <- cluster_merge[3]
  cluster_label
}

마지막으로, 현재 군집해로부터 가장 최적의 다음단계 군집해를 얻는 사용자 함수 best_merge_cluster를 아래와 같이 구현해보자.

  1. generate_clusters를 실행하여 다음 단계에 가능한 모든 군집해를 구한다.
  2. 1의 각 군집해에 함수 calculate_ssw를 적용하여 \(SSW\)값을 구한다.
  3. \(SSW\)값이 최소인 군집해를 최적 군집해로 선정한다.
# 최적 군집 결합
best_merge_cluster <- function(df, cluster_label) {
  candidate_solutions <- generate_clusters(cluster_label)
  ssw <- sapply(candidate_solutions, function(x) calculate_ssw(df, x))
  list(
    new_cluster_label = candidate_solutions[[which.min(ssw)]],
    new_ssw = min(ssw)
  )
}

위 사용자 함수들을 이용하여 Table 12.3에 대한 워드 군집 분석을 수행해보자.

#단계0
init_cluster <- tibble(
  id = train_df$id,
  cluster = as.character(1:nrow(train_df))
)
i <- 0L
current_clusters <- unique(init_cluster$cluster)
k <- length(current_clusters)
ssw <- calculate_ssw(train_df, init_cluster)

print_clusters <- function(i, k, clusters, ssw) {
  cat("Iteration: ", i, ", k = ", k, ", clusters = ", paste0("{", clusters, "}"), ", SSW =", ssw, "\n")
}

print_clusters(i, k, current_clusters, ssw)
## Iteration:  0 , k =  8 , clusters =  {1} {2} {3} {4} {5} {6} {7} {8} , SSW = 0
#단계1
iteration <- vector("list", length = nrow(train_df) - 1)
while(k > 1) {
  i <- i + 1
  if(i == 1) {
    iteration[[i]] <- best_merge_cluster(
      train_df,
      init_cluster
    )
  } else {
    iteration[[i]] <- best_merge_cluster(
      train_df,
      iteration[[i-1]]$new_cluster_label
    )
  }

  current_clusters <- unique(iteration[[i]]$new_cluster_label$cluster)
  k <- length(current_clusters)
  ssw <- iteration[[i]]$new_ssw
  
  print_clusters(i, k, current_clusters, ssw)
}
## Iteration:  1 , k =  7 , clusters =  {1} {2,7} {3} {4} {5} {6} {8} , SSW = 1 
## Iteration:  2 , k =  6 , clusters =  {1,3} {2,7} {4} {5} {6} {8} , SSW = 3.5 
## Iteration:  3 , k =  5 , clusters =  {1,3} {2,7} {4,8} {5} {6} , SSW = 6 
## Iteration:  4 , k =  4 , clusters =  {1,3} {2,7,5} {4,8} {6} , SSW = 23.66667 
## Iteration:  5 , k =  3 , clusters =  {1,3,6} {2,7,5} {4,8} , SSW = 43.16667 
## Iteration:  6 , k =  2 , clusters =  {1,3,6} {2,7,5,4,8} , SSW = 140.4 
## Iteration:  7 , k =  1 , clusters =  {1,3,6,2,7,5,4,8} , SSW = 499.875

12.4.3 R 패키지 내 워드 방법

R 패키지로 구현된 워드 군집은 위에서 구현한 \(SSW\)와는 다소 다른 metric을 이용하여 군집해를 구한다. 따라서, 우선 워드 방법이 제안된 논문들을 살펴볼 필요가 있다.

우선 원 논문 Ward Jr (1963) 는 \(ESS\)(error sum of squares)를 아래와 같이 정의하였으며, 이는 위에서 사용한 \(SSW\)와 일치한다.

\[\begin{equation*} \begin{split} ESS(\{C_1, \cdots, C_k \}) &= \sum_{i = 1}^{k} ESS(C_i)\\ &= \sum_{i = 1}^{k} \sum_{u \in C_i} \mathbf{x}_u^\top \mathbf{x}_u - |C_i| \mathbf{c}_i^\top \mathbf{c}_i\\ &= SSW \end{split} \end{equation*}\]

위 식에서 임의의 두 군집 \(C_i\), \(C_j\)를 하나의 군집으로 묶을 때 \(SSW\)의 변화는 아래와 같다. \(C_i\)와 \(C_j\) 외의 군집은 \(SSW\)의 변화에 영향을 미치지 않으므로, \(SSW\) 변화량은 아래와 같이 군집 \(C_i\)와 \(C_j\)에 속하는 객체만을 이용하여 구할 수 있으며, 결과적으로 \(C_i\)와 \(C_j\)의 군집 크기 \(|C_i|\)와 \(|C_j|\)및 군집 중심벡터 \(\mathbf{c}_i\)와 \(\mathbf{c}_j\)를 이용하여 구할 수 있다.

\[\begin{equation} \begin{split} \Delta SSW =& ESS(C_i \cup C_j) - ESS(C_i) - ESS(C_j)\\ =& \sum_{u \in C_i \cup C_j} \mathbf{x}_u^\top \mathbf{x}_u - (|C_i| + |C_j|)\left[\frac{|C_i|\mathbf{c}_i + |C_j|\mathbf{c}_j}{|C_i| + |C_j|}\right]^\top \left[\frac{|C_i|\mathbf{c}_i + |C_j|\mathbf{c}_j}{|C_i| + |C_j|}\right]\\ & - \left( \sum_{u \in C_i} \mathbf{x}_u^\top \mathbf{x}_u - |C_i| \mathbf{c}_i^\top \mathbf{c}_i \right) - \left( \sum_{u \in C_j} \mathbf{x}_u^\top \mathbf{x}_u - |C_j| \mathbf{c}_j^\top \mathbf{c}_j \right)\\ =& -\frac{1}{|C_i| + |C_j|} \left( |C_i|\mathbf{c}_i + |C_j|\mathbf{c}_j \right)^\top \left( |C_i|\mathbf{c}_i + |C_j|\mathbf{c}_j \right) + |C_i| \mathbf{c}_i^\top \mathbf{c}_i + |C_j| \mathbf{c}_j^\top \mathbf{c}_j\\ =& \frac{|C_i||C_j|}{|C_i| + |C_j|} \left(\mathbf{c}_i - \mathbf{c}_j\right)^\top \left(\mathbf{c}_i - \mathbf{c}_j\right) \end{split} \tag{12.1} \end{equation}\]

따라서 워드 방법은 각 iteration에서 식 (12.1)를 최소화하는 두 군집 \(C_i\), \(C_j\)를 선택하여 두 군집을 하나로 묶는 방법이다.

한편, \(SS(C_i)\)는 아래와 같이 군집 \(C_i\)내 객체들 간의 제곱 유클리드 거리로 나타낼 수 있다.

\[\begin{equation} \begin{split} D^2(C_i) =& \sum_{u, v \in C_i} (\mathbf{x}_u - \mathbf{x}_v)^\top (\mathbf{x}_u - \mathbf{x}_v)\\ =& \sum_{u, v \in C_i} \left((\mathbf{x}_u - \mathbf{c}_i) - (\mathbf{x}_v - \mathbf{c}_i)\right)^\top \left((\mathbf{x}_u - \mathbf{c}_i) - (\mathbf{x}_v - \mathbf{c}_i)\right)\\ =& 2 \sum_{u \in C_i} (\mathbf{x}_u - \mathbf{c}_i)^\top (\mathbf{x}_u - \mathbf{c}_i) - 2 \sum_{u, v \in C_i} (\mathbf{x}_u - \mathbf{c}_i)^\top (\mathbf{x}_v - \mathbf{c}_i)\\ =& 2 \sum_{u \in C_i} (\mathbf{x}_u - \mathbf{c}_i)^\top (\mathbf{x}_u - \mathbf{c}_i)\\ =& 2 SS(C_i) \end{split} \tag{12.2} \end{equation}\]

위 식 (12.2)을 달리 표현하면, 객체간의 제곱 유클리드 거리를 표현한 행렬에서 군집 \(i\)에 속한 객체들에 해당하는 부분행렬(submatrix)를 뽑아 행렬의 원소값을 모두 더하면, 그 값이 \(2 SS(C_i)\)와 같다. 이를 통해 각 군집의 중심벡터를 계산하지 않고도 각 iteration에서 SSW를 최소화하는 군집 결합을 찾을 수 있다.

R 패키지 stats 내의 hclust 함수는 워드 방법으로 method 파라미터의 값을 “ward.D” 혹은 “ward.D2”로 설정할 수 있다. 이 두 방법의 차이는 입력 거리행렬을 제곱 유클리드 거리로 사용하는지 일반 유클리드 거리로 사용하는지의 차이로, 아래에서 R 스크립트 예제와 함께 설명하기로 한다.

우선 method값을 “ward.D2”로 설정하는 경우, dist 함수의 결과를 입력 거리행렬로 그대로 사용하면 된다.

res_ward.D2 <- dist(train_df[, -1]) %>%
  hclust(method = "ward.D2")

이 때, 결과 데이터 res_ward.D2에서 워드 방법의 criterion을 나타내는 height 원소(component)가 표현하는 값은 위에서 계산하였던 \(SSW\)와 다르다.

res_ward.D2$height
## [1]  1.414214  2.236068  2.236068  5.944185  6.244998
## [6] 13.945131 26.813243

이는 height에서 표현하는 값은 전체 \(SSW\)가 아니라, 두 군집 \(i\)와 \(j\)를 하나로 묶을 때 추가로 증가하는 \(SSW\) 수치의 변환으로, 아래와 같이 계산되기 때문이다.

\[\begin{equation} height = \sqrt{D^2(C_i \cup C_j) - \left(D^2(C_i) + D^2(C_j)\right)} \tag{12.3} \end{equation}\]

따라서, 군집 \(i\)와 \(j\)를 하나로 묶을 때 증가하는 \(SSW\)의 수치 \(\Delta SSW\)는 아래와 같이 표현된다.

\[\begin{equation} \Delta SSW = \frac{1}{2} height^2 \end{equation}\]

각 iteration에서 발생하는 \(\Delta SSW\)의 누적합이 위 12.4.2절에서 보였던 \(SSW\) 결과와 동일함을 아래와 같이 확인해보자.

tibble(
  iteration = c(1:(nrow(train_df) - 1)),
  height = res_ward.D2$height
) %>%
  mutate(
    delta_ssw = height ^ 2 / 2
  ) %>%
  mutate(
    ssw = cumsum(delta_ssw)
  ) %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r', 'r'),
    col.names = c('iteration', '$height$', '$\\Delta SSW = \\frac{1}{2} height ^ 2$', '$SSW = \\sum \\Delta SSW$'),
    caption = 'hclust 함수 ward.D2 방법의 height와 SSW 관계'
  )
Table 12.4: hclust 함수 ward.D2 방법의 height와 SSW 관계
iteration \(height\) \(\Delta SSW = \frac{1}{2} height ^ 2\) \(SSW = \sum \Delta SSW\)
1 1.414214 1.00000 1.00000
2 2.236068 2.50000 3.50000
3 2.236068 2.50000 6.00000
4 5.944185 17.66667 23.66667
5 6.244998 19.50000 43.16667
6 13.945131 97.23333 140.40000
7 26.813243 359.47500 499.87500

우선 method값을 “ward.D”로 설정하는 경우, dist 함수의 결과를 입력 거리행렬로 그대로 사용하면 아래와 같이 위 “ward.D2”와는 다른 height값을 출력하며, 이는 워드 방법의 criterion을 정확히 반영하지 못한다.

res_ward.D <- dist(train_df[, -1]) %>%
  hclust(method = "ward.D")

res_ward.D$height
## [1]  1.414214  2.236068  2.236068  6.452039  6.615990
## [6] 17.358484 39.311447

이는 “ward.D2”는 워드 방법 수행 전 입력된 유클리드 거리행렬을 내부적으로 제곱하는 반면, “ward.D” 방법은 제곱 유클리드 거리행렬이 입력되는 것을 가정하기 때문이다.

Lance and Williams (1967) 은 군집 \(i\)와 \(j\)를 하나로 묶을 때, 새로 생성된 군집과 다른 군집들간의 거리는 원 두 군집들과 다른 군집들간의 거리로 아래와 같이 표현됨을 보였다. 이를 Lance-Williams update 공식이라 한다.

\[\begin{equation} D(C_i \cup C_j, C_{h \notin \{i, j\}}) = \alpha_i D(C_i, C_h) + \alpha_j D(C_j, C_h) + \beta D(C_i, C_j) + \gamma |D(C_i, C_h) - D(C_j, C_h)| \tag{12.4} \end{equation}\]

이후 Wishart (1969) 에서 워드 방법을 위 Lance-Williams update 공식으로 표현하였다.

\[\begin{equation} \begin{split} \alpha_i =& \frac{|C_i| + |C_h|}{|C_i| + |C_j| + |C_h|}\\ \alpha_j =& \frac{|C_j| + |C_h|}{|C_i| + |C_j| + |C_h|}\\ \beta =& - \frac{|C_h|}{|C_i| + |C_j| + |C_h|}\\ \gamma =& 0 \end{split} \tag{12.5} \end{equation}\]

이 때, 식 (12.5)가 기반한 식 (12.4)에서의 거리함수 \(D\)는 제곱 유클리드 거리를 사용한다.

“ward.D” 방법은 제곱 유클리드 거리의 입력을 가정하며, 위의 경우와 같이 제곱 유클리드 거리가 아닌 일반 유클리드 거리행렬을 입력하였을 때, 오류 메시지를 출력하는 대신, 입력된 거리행렬이 제곱 유클리드 거리를 나타낸다 가정하고 Lance-Williams update를 수행한다. 따라서, 이 경우 height는 워드 방법의 criterion을 정확히 표현하지 못한다.

제곱 유클리드 거리를 “ward.D” 방법의 입력 거리행렬로 설정하고, 구해진 height를 출력해보자

res_ward.D <- dist(train_df[, -1])^2 %>%
  hclust(method = "ward.D")

res_ward.D$height
## [1]   2.00000   5.00000   5.00000  35.33333  39.00000
## [6] 194.46667 718.95000

위 height값은 “ward.D2” 방법에서 출력된 값보다 크다. 위 값의 제곱근(square root)를 구하면 “ward.D2”에서의 height값과 동일한 값을 얻을 수 있다.

sqrt(res_ward.D$height)
## [1]  1.414214  2.236068  2.236068  5.944185  6.244998
## [6] 13.945131 26.813243

제곱 유클리드 거리행렬을 입력한 “ward.D” 방법의 결과로 출력된 criterion height는 \(2 \Delta SSW\)의 값에 해당하는 수치이며, 각 iteration 당 \(\sum_i D(C_i)\)의 값의 변화량이라고 볼 수 있다. (식 (12.2) 참조)

tibble(
  iteration = c(1:(nrow(train_df) - 1)),
  height = res_ward.D$height
) %>%
  mutate(
    delta_ssw = height / 2
  ) %>%
  mutate(
    ssw = cumsum(delta_ssw)
  ) %>%
  knitr::kable(
    booktabs = TRUE,
    align = c('r', 'r', 'r', 'r'),
    col.names = c('iteration', '$height$', '$\\Delta SSW = \\frac{1}{2} height$', '$SSW = \\sum \\Delta SSW$'),
    caption = 'hclust 함수 ward.D 방법의 height와 SSW 관계'
  )
Table 12.5: hclust 함수 ward.D 방법의 height와 SSW 관계
iteration \(height\) \(\Delta SSW = \frac{1}{2} height\) \(SSW = \sum \Delta SSW\)
1 2.00000 1.00000 1.00000
2 5.00000 2.50000 3.50000
3 5.00000 2.50000 6.00000
4 35.33333 17.66667 23.66667
5 39.00000 19.50000 43.16667
6 194.46667 97.23333 140.40000
7 718.95000 359.47500 499.87500

즉, “ward.D2”와 “ward.D”의 가장 큰 차이는 입력될 거리행렬이 유클리드 거리(ward.D2)인지 제곱 유클리드 거리(ward.D)인지의 차이이다.

참고로, cluster 패키지의 agnes함수도 워드 방법을 지원하며, 이 경우 파라미터 method의 값을 “ward”로 설정한 결과가 hclust함수의 “ward.D2”의 경우와 동일하다. 본 절에서는 해당 함수의 자세한 사용법은 생략한다.

res_agnes_ward <- cluster::agnes(train_df[, -1], method = "ward")

sort(res_agnes_ward$height)
## [1]  1.414214  2.236068  2.236068  5.944185  6.244998
## [6] 13.945131 26.813243

12.5 분리적 방법 - 다이아나

다이아나는 분리적 방법의 하나로, Kaufman and Rousseeuw (1990) 에 의하여 제안된 것이다. 이는 전체의 객체를 하나의 군집으로 시작하여 매번 이분화하는 등 모든 군집이 단독 객체로 구성될 때까지 진행하는 방법이다. 이 때, 비유사성 척도로는 평균거리를 사용한다.

12.5.1 기본 R 스크립트

train_df <- tibble(
  id = c(1:7),
  x1 = c(30, 45, 25, 40, 50, 20, 42),
  x2 = c(15, 22, 12, 24, 25, 10, 9)
)

knitr::kable(train_df, booktabs = TRUE,
             align = c('r', 'r', 'r'),
             col.names = c('객체번호', '$x_1$', '$x_2$'),
             caption = 'DIANA 군집 대상 객체 데이터')
Table 12.6: DIANA 군집 대상 객체 데이터
객체번호 \(x_1\) \(x_2\)
1 30 15
2 45 22
3 25 12
4 40 24
5 50 25
6 20 10
7 42 9

Table 12.6와 같이 두 변수 \(x_1\), \(x_2\)로 이루어진 7개의 객체 데이터에 대해 DIANA 방법에 의해 군집해를 아래와 같이 cluster 패키지의 diana 함수를 이용하여 간단히 구할 수 있다.

res_diana <- cluster::diana(train_df[, -1])
cluster::pltree(res_diana,
                main = NULL,
                xlab = "observation"
                )
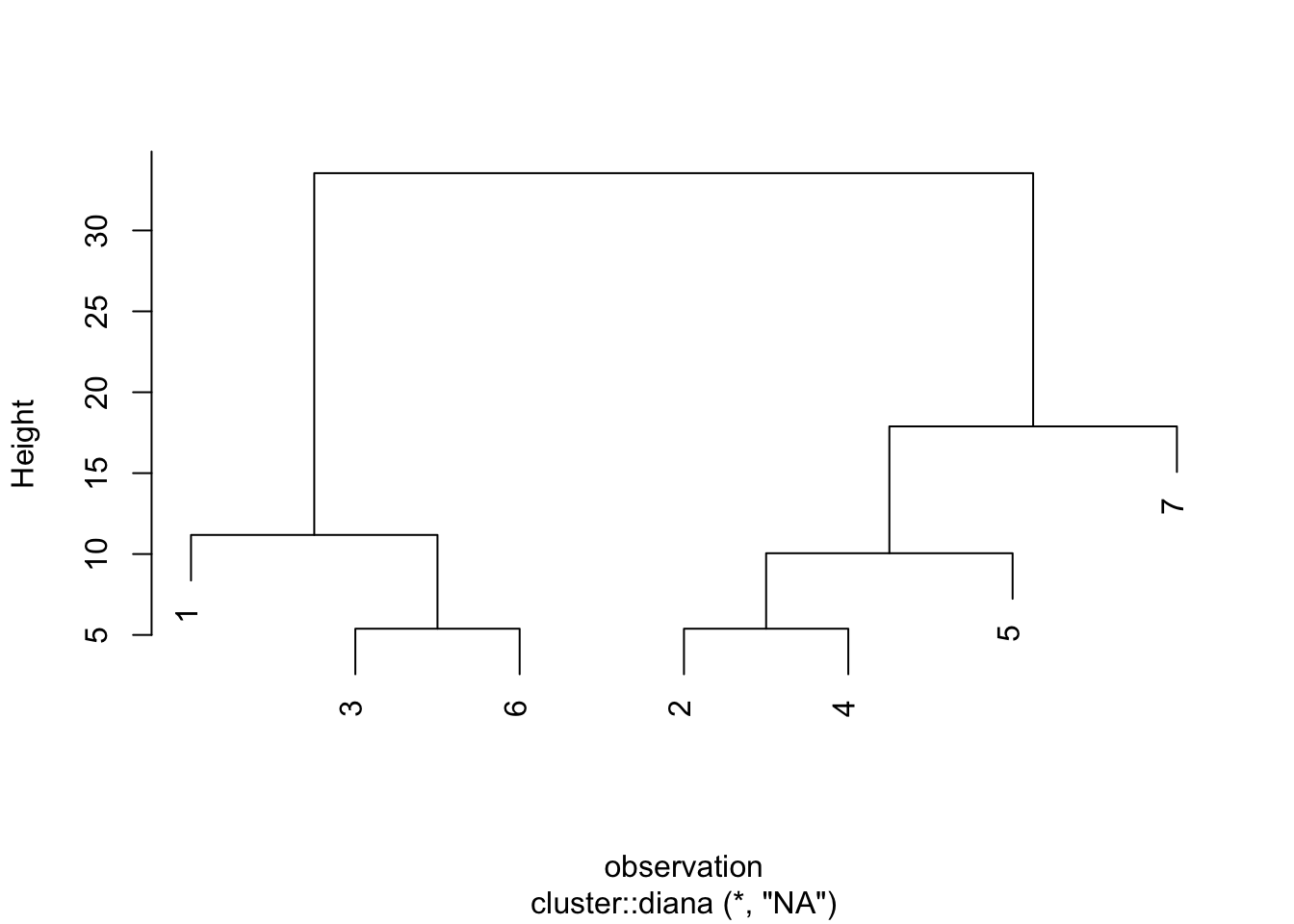
DIANA 방법에 의한 군집 덴드로그램

Figure 12.4: DIANA 방법에 의한 군집 덴드로그램

12.5.2 다이아나 알고리즘

가장 처음 이분화가 이루어질 때, 우선 타 객체와의 평균거리가 가장 큰 객체가 분파되어 새로운 군집을 형성한다. 그리고 다른 객체에 대하여, 군집에 남아있을 때의 평균거리와 새로운 군집으로 분리될 때의 평균거리를 산출하여, 현 군집에 잔류 또는 새로운 군집으로의 합류를 결정한다.

여기서 객체 \(i\)와 군집 \(C\)간의 평균거리는 다음과 같이 산출된다.

\[\begin{equation*} \bar{d}(i, C) = \begin{cases} \frac{1}{|C| - 1} \sum_{j \in C} d(i, j) & \text{ if } i \in C\\ \frac{1}{|C|} \sum_{j \in C} d(i, j) & \text{ if } i \notin C \end{cases} \end{equation*}\]

본 방법의 알고리즘은 다음과 같다.

  1. 단계0: \(n\)개의 객체를 하나의 군집으로 간주한다. (\(k = 1\))
  2. 단계1: 객체 간 거리가 가장 큰 두 객체를 포함한 군집을 이분화 대상으로 선정한다. (이를 \(A\)라 하고, \(B \leftarrow \emptyset\)로 둔다.)
  3. 단계2: 다음 과정을 통하여 군집 \(A\)를 이분화한다.
    1. 단계2-1: \(i \leftarrow \arg\,\max_{i'} \bar{d}(i', A)\)
    2. 단계2-2: \(A \leftarrow A - \{i\}\), \(B \leftarrow B \cup \{i\}\)
    3. 단계2-3: \(i \leftarrow \arg\,\max_{i' \in A} e(i') = \bar{d}(i', A) - \bar{d}(i', B)\)
    4. 단계2-4: \(e(i) > 0\)이면 단계2-2로, \(e(i) \le 0\)이면 단계3으로
  4. 단계3
    1. \(k \leftarrow k + 1\)
    2. \(k < n\)이면 단계1로, \(k = n\)이면 Stop.

DIANA 알고리즘을 R script로 구현해보자.

우선, 단계1의 군집을 찾는 함수 max_distance_cluster를 구현하자. 이 함수는 아래 두 개의 데이터 프레임을 입력받는다.

  • 입력
    • df: 관측 데이터. 각 열의 설명은 아래와 같다.
      • id: 객체번호
      • 나머지 열: 숫자형 변수
    • cluster_label: 각 객체의 현재 소속 군집을 나타내는 데이터 프레임
      • id: 객체번호
      • cluster: 군집명
  • 함수값
    • cluster: 객체간 거리가 가장 큰 두 객체를 포함한 군집명
    • distance: 군집 내 객체간 최대 거리
max_distance_cluster <- function(df, cluster_label) {
  unique_cluster <- unique(cluster_label$cluster)
  
  cluster_df <- lapply(unique_cluster, function(x) {
    cluster_label %>% 
      filter(cluster == x) %>%
      inner_join(df, by = "id") %>%
      select(-cluster, -id)
    })
  
  max_distance <- sapply(cluster_df, 
                         function(x) {
                           if(nrow(x) == 1) return(0)
                           max(dist(x))
                         }
                         )

  list(
    cluster = unique_cluster[which.max(max_distance)],
    distance = max(max_distance)
  )
}

단계 2-1에서 군집 내 평균거리가 가장 큰 객체를 찾는 함수 max_within_distance를 아래와 같이 구현해보자. 이 때 입력변수인 cluster_df는 해당 군집의 객체 데이터로, 객체 번호를 나타내는 열 id와 객체의 각 숫자형 변수를 표현하는 열들로 구성된다.

max_within_distance <- function(cluster_df) {
  idx <- dist(subset(cluster_df, select = -id), upper = TRUE) %>%
    broom::tidy() %>%
    group_by(item1) %>%
    summarize(mean_distance = mean(distance)) %>%
    ungroup() %>%
    arrange(-mean_distance) %>%
    .[["item1"]] %>%
    .[1]
  
  cluster_df$id[idx]
}

이후 단계2-3에서 정의한 \(e(i') = \bar{d}(i', A) - \bar{d}(i', B)\)를 계산하는 함수 e_score를 아래와 같이 구현한다.

  • object: 객체 번호(id)
  • A(B): 군집 \(A\)(\(B\))의 객체 데이터. 행은 객체를 나타내며, id 열은 객체 번호, 이외의 열들은 변수를 나타낸다.
e_score <- function(object, A, B) {
  d_from_A <- proxy::dist(subset(A, id == object, -id), 
                          subset(A, id != object, -id)) %>% 
    mean()
  d_from_B <- proxy::dist(subset(A, id == object, -id), 
                          B %>% select(-id)) %>% 
    mean()
  return(d_from_A - d_from_B)
}

위 두 함수 max_within_distance와 e_score를 이용하여, 주어진 데이터 프레임을 두 군집으로 나누는 함수 split_cluster를 구현해보자.

  • 입력: 객체 데이터를 나타내는 데이터 프레임 cluster_df. 행은 객체를 나타내며, 객체 번호를 나타내는 열 id와 객체의 각 숫자형 변수를 표현하는 열들로 구성된다.
  • 함수값: 아래 두 개의 component를 지닌 리스트.
    • idx_A: 객체 데이터에서 행렬 \(A\)에 속하는 객체 번호
    • idx_B: 객체 데이터에서 행렬 \(B\)에 속하는 객체 번호
split_cluster <- function(cluster_df) {
  n <- nrow(cluster_df)
  
  idx_A <- cluster_df$id
  idx_B <- NULL
  
  # 단계2-1
  max_object <- max_within_distance(cluster_df)
  e_i <- Inf

  while(e_i > 0) {
    # 단계2-2
    idx_B <- c(idx_B, max_object)
    idx_A <- setdiff(idx_A, max_object)
    
    A <- cluster_df %>% filter(id %in% idx_A)
    B <- cluster_df %>% filter(id %in% idx_B)

    # 단계2-3
    if(nrow(A) > 1) {
      e_is <- sapply(A$id, function(x) e_score(x, A, B))
      max_object <- A$id[which.max(e_is)]
      e_i <- max(e_is)
    } else {
      e_i <- -Inf
    }
  }
  
  return(list(idx_A = idx_A, idx_B = idx_B))
}

단계1 함수 max_distance_cluster와 단계2 함수 split_cluster를 반복적으로 수행하며 각각의 객체가 군집에 될 때까지 군집을 분리해간다.

# 단계0
current_cluster <- tibble(
  id = train_df$id
)
current_cluster$cluster <- paste(1:nrow(current_cluster), collapse = ",")
i <- 0L
k <- 1L

while(k < nrow(train_df)) {
  i <- i + 1L
  
  # 단계1
  max_cluster <- max_distance_cluster(train_df, current_cluster)

  # 단계2
  new_split <- current_cluster %>%
    filter(cluster == max_cluster$cluster) %>%
    inner_join(train_df, by = "id") %>%
    select(-cluster) %>%
    split_cluster()

  # 군집해 업데이트
  current_cluster[
    current_cluster$id %in% new_split$idx_A, 
    "cluster"] <- paste(new_split$idx_A, collapse = ",")
  current_cluster[
    current_cluster$id %in% new_split$idx_B, 
    "cluster"] <- paste(new_split$idx_B, collapse = ",")
  
  # 군집해 출력
  k <- length(unique(current_cluster$cluster))
  cat("Iteration: ", i, ", k = ", k, ", clusters = ", 
      paste0("{", unique(current_cluster$cluster), "}"),
      ", height = ", max_cluster$distance, "\n")
}
## Iteration:  1 , k =  2 , clusters =  {6,3,1} {2,4,5,7} , height =  33.54102 
## Iteration:  2 , k =  3 , clusters =  {6,3,1} {2,4,5} {7} , height =  17.88854 
## Iteration:  3 , k =  4 , clusters =  {1} {2,4,5} {3,6} {7} , height =  11.18034 
## Iteration:  4 , k =  5 , clusters =  {1} {2,4} {3,6} {5} {7} , height =  10.04988 
## Iteration:  5 , k =  6 , clusters =  {1} {2} {3,6} {4} {5} {7} , height =  5.385165 
## Iteration:  6 , k =  7 , clusters =  {1} {2} {3} {4} {5} {6} {7} , height =  5.385165

위 출력 결과에서 height는 해당 iteration에서 분리된 군집의 분리 전 지름(diameter)으로, 함수 max_distance_cluster에서 계산한 군집 내 객체간 최대 거리를 나타내며, 이는 R 패키지 cluster의 diana 함수 수행 시 함수값으로 출력되는 height값이다. Iteration이 진행됨에 따라 height의 값이 감소하는 것을 확인할 수 있다.

12.6 군집수의 결정

최적의 군집수를 결정하는 객관적인 방법은 존재하지 않는다. 계층적 군집방법에서는 덴드로그램을 참조하여 군집 간의 거리가 급격히 증가하는 계층에서 수평으로 절단하여, 그 이하의 그룹들을 하나의 군집으로 형성하는 방안을 널리 사용하고 있다. 이외에 군집수를 결정하는 데 통계량으로 다음과 같은 통계량들이 부수적으로 사용된다.

  1. 새 군집의 RMS 표준편차(root-mean-square standard deviation of the new cluster; RMSSTD)

\[\begin{equation*} RMSSTD(C_i, C_j) = \sqrt{\frac{SS(C_i \cup C_j)}{p(|C_i| + |C_j| - 1)}} \end{equation*}\]

  1. Semipartial R-squared(SPR)

\[\begin{equation*} SPR(C_i, C_j) = \frac{SS(C_i \cup C_j) - (SS(C_i) + SS(C_j))}{SST} \end{equation*}\]

where

\[\begin{equation*} SST = \sum_{i = 1}^{n} \sum_{j = 1}^{p} \left( x_{ji} - \frac{1}{n} \sum_{a = 1}^{n} x_{ja} \right)^2 \end{equation*}\]

  1. R-squared(\(R^2\))

\[\begin{equation*} 1 - \frac{\sum_{i = 1}^{k} SS(C_i)}{SST} \end{equation*}\]

위 12.4.2절에서 워드 군집 알고리즘으로 구현한 군집 과정에 대해 위 통계량을 계산해보자.

train_df <- tibble(
  id = c(1:8),
  x1 = c(4, 20, 3, 19, 17, 8, 19, 18),
  x2 = c(15, 13, 13, 4, 17, 11, 12, 6)
)

sst <- train_df %>%
  select(-id) %>%
  sapply(function(x) sum((x - mean(x))^2)) %>%
  sum()

#단계0
init_cluster <- tibble(
  id = train_df$id,
  cluster = as.character(1:nrow(train_df))
)
i <- 0L
current_clusters <- unique(init_cluster$cluster)
k <- length(current_clusters)
ssw <- calculate_ssw(train_df, init_cluster)
old_ssw <- NA_real_

#단계1
iteration <- vector("list", length = nrow(train_df) - 1)
while(k > 1) {
  i <- i + 1
  old_ssw <- ssw
  
  if(i == 1) {
    old_cluster <- init_cluster
  } else {
    old_cluster <- iteration[[i-1]]$new_cluster_label
  }
  
  iteration[[i]] <- best_merge_cluster(
    train_df,
    old_cluster
  )
  
  merged <- old_cluster %>% 
    anti_join(iteration[[i]]$new_cluster_label, by = "cluster")
  
  current_clusters <- unique(iteration[[i]]$new_cluster_label$cluster)
  k <- length(current_clusters)
  ssw <- iteration[[i]]$new_ssw
  
  iteration[[i]]$rmsstd <- sqrt(
    merged %>% 
      inner_join(train_df, by = "id") %>%
      select(-id, -cluster) %>%
      sapply(function(x) sum((x - mean(x))^2)) %>%
      sum() / (2 * (nrow(merged) - 1))
  )
  
  iteration[[i]]$iter <- i
  iteration[[i]]$merge <- paste0("{", unique(merged$cluster), "}", collapse = ", ")
  iteration[[i]]$sol <- paste0("{", unique(current_clusters), "}", collapse = ", ")
  iteration[[i]]$spr <- (ssw - old_ssw) / sst
  iteration[[i]]$r_sq <- 1 - ssw / sst
}
cluster_statistic <- lapply(iteration, function(x) x[
  c("iter", "merge", "sol", "rmsstd", "spr", "r_sq")]) %>%
  bind_rows(
    tibble(
      iter = 0,
      sol = paste0("{", unique(init_cluster$cluster), "}", collapse = ", "),
      r_sq = 1
    )
  ) %>%
  arrange(iter)

cluster_statistic %>%
  knitr::kable(
    booktabs = TRUE,
    col.names = c('Iteration', '통합대상군집', '통합 후 군집',
                  '$RMSSTD$', '$SPR$', '$R^2$'),
    caption = '군집 과정에 따른 여러 통계량'
  )
Table 12.7: 군집 과정에 따른 여러 통계량
Iteration 통합대상군집 통합 후 군집 \(RMSSTD\) \(SPR\) \(R^2\)
0 NA {1}, {2}, {3}, {4}, {5}, {6}, {7}, {8} NA NA 1.0000000
1 {2}, {7} {1}, {2,7}, {3}, {4}, {5}, {6}, {8} 0.7071068 0.0020005 0.9979995
2 {1}, {3} {1,3}, {2,7}, {4}, {5}, {6}, {8} 1.1180340 0.0050013 0.9929982
3 {4}, {8} {1,3}, {2,7}, {4,8}, {5}, {6} 1.1180340 0.0050013 0.9879970
4 {2,7}, {5} {1,3}, {2,7,5}, {4,8}, {6} 2.1602469 0.0353422 0.9526548
5 {1,3}, {6} {1,3,6}, {2,7,5}, {4,8} 2.3452079 0.0390098 0.9136451
6 {2,7,5}, {4,8} {1,3,6}, {2,7,5,4,8} 3.8470768 0.1945153 0.7191298
7 {1,3,6}, {2,7,5,4,8} {1,3,6,2,7,5,4,8} 5.9753960 0.7191298 0.0000000 
cluster_statistic %>%
  mutate(
    rmsstd = if_else(is.na(rmsstd), 0, rmsstd),
    spr = if_else(is.na(spr), 0, spr)
    ) %>%
  ggplot(aes(x = iter)) +
  geom_line(aes(y = rmsstd, color = "RMSSTD")) +
  geom_line(aes(y = spr * 6, color = "SPR")) + 
  geom_line(aes(y = r_sq * 6, color = "R2")) + 
  scale_y_continuous(sec.axis = sec_axis(~ . / 6, name = "SPR, R2")) +
  ylab("RMSSTD") +
  xlab("Iteration")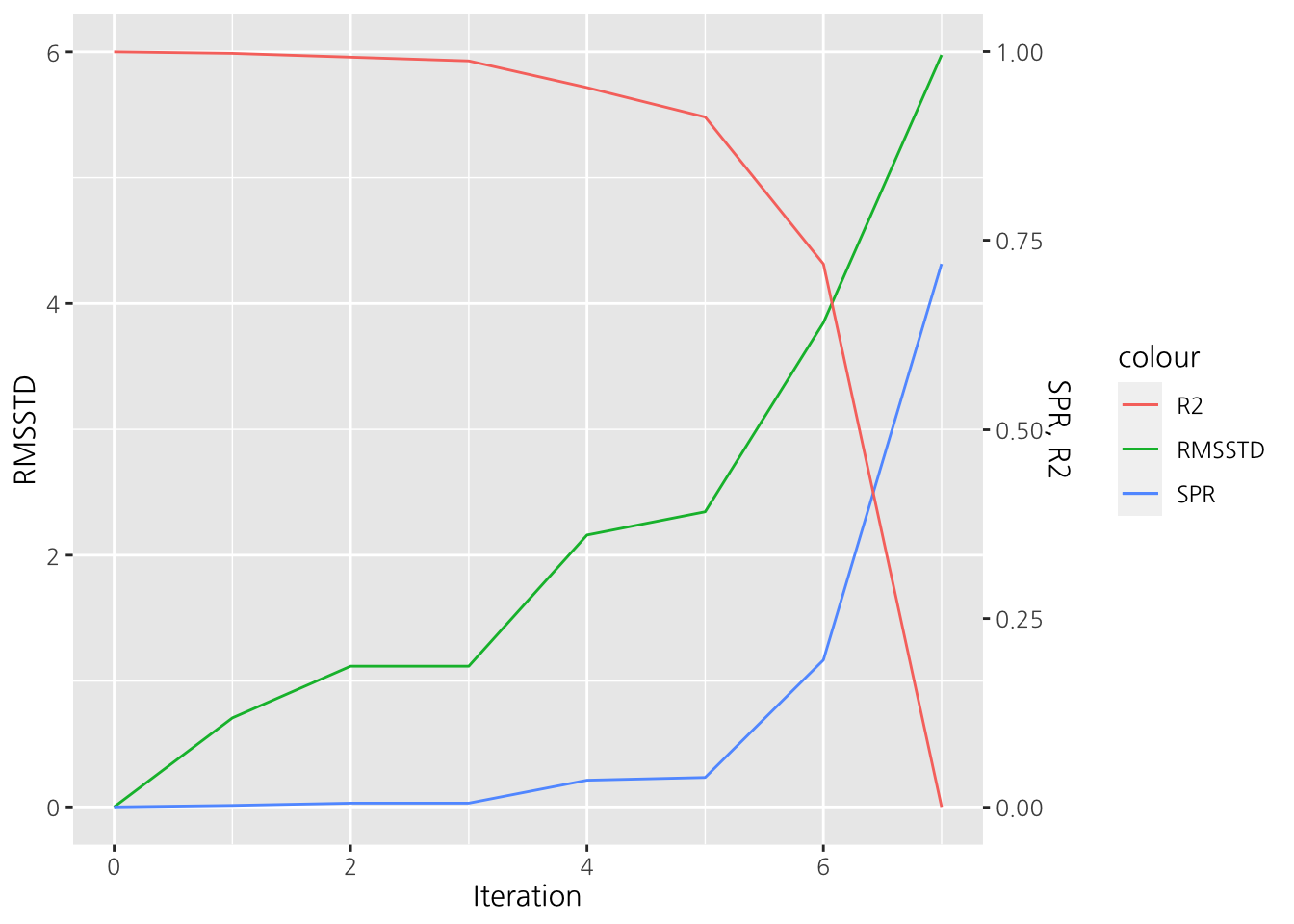
군집 과정에 따른 통계량 추이

Figure 12.5: 군집 과정에 따른 통계량 추이

그림 12.5에서 보듯이 Iteration 6부터 3가지 통계량 모두 급격하게 변화하는 것을 알 수 있다. 따라서 군집수는 Iteration 5까지 3개가 가장 적당하다고 하겠다.

References

Kaufman, L, and P. J. Rousseeuw. 1990. “Finding Groups in Data: An Introduction to Cluster Analysis.”
Lance, Godfrey N, and William Thomas Williams. 1967. “A General Theory of Classificatory Sorting Strategies: 1. Hierarchical Systems.” The Computer Journal 9 (4): 373–80.
Ward Jr, Joe H. 1963. “Hierarchical Grouping to Optimize an Objective Function.” Journal of the American Statistical Association 58 (301): 236–44.
Wishart, David. 1969. “256. Note: An Algorithm for Hierarchical Classifications.” Biometrics, 165–70.