Chapter 2 회귀분석
2.1 필요 R 패키지 설치
본 장에서 필요한 R 패키지들은 아래와 같다.
| package | version |
|---|---|
| tidyverse | 1.3.1 |
| stats | 4.1.3 |
| broom | 0.7.8 |
2.2 다중회귀모형
아래와 같이 \(n\)개의 객체와 \(k\)개의 독립변수(\(\mathbf{x}\))로 이루어지고 하나의 종속변수(\(y\))로 이루어진 선형 회귀모형을 정의하자.
\[\begin{equation} y_i = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \cdots + \beta_k x_{ik} + \epsilon_i \tag{2.1} \end{equation}\]
이 때, 오차항 \(\epsilon_i\)은 서로 독립이고 동일한 정규분포 \(N(0, \sigma^2)\)을 따른다.
위 회귀모형은 아래와 같이 행렬의 연산으로 표한할 수 있다.
\[\begin{equation} \mathbf{y} = \mathbf{X} \boldsymbol{\beta} + \boldsymbol{\epsilon} \tag{2.2} \end{equation}\]
이 때,
\[ \mathbf{y} = \left[ \begin{array}{c} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{array} \right] \]
\[ \mathbf{X} = \left[ \begin{array}{c c c c c} 1 & x_{11} & x_{12} & \cdots & x_{1k}\\ 1 & x_{21} & x_{22} & \cdots & x_{2k}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nk} \end{array} \right] \]
\[ \boldsymbol{\beta} = \left[ \begin{array}{c} \beta_0 \\ \beta_1 \\ \beta_2 \\ \vdots \\ \beta_k \end{array} \right] \]
\[ \boldsymbol{\epsilon} = \left[ \begin{array}{c} \epsilon_1 \\ \epsilon_2 \\ \epsilon_3 \\ \vdots \\ \epsilon_n \end{array} \right] \]
로 정의되며,
\[ E[\boldsymbol{\epsilon}] = \mathbf{0}, \, Var[\boldsymbol{\epsilon}] = \sigma^2 \mathbf{I} \]
이다.
2.3 반응치에 대한 추정 및 예측
2.3.1 평균반응치의 추정
2.3.1.1 기본 R 스트립트
다음과 같은 10명의 나이(age), 키(height), 몸무게(weight)에 대한 데이터가 있다.
train_df <- tribble(
~age, ~height, ~weight,
21, 170, 60,
47, 167, 65,
36, 173, 67,
15, 165, 54,
54, 168, 73,
25, 177, 71,
32, 169, 68,
18, 172, 62,
43, 171, 66,
28, 175, 68
)
knitr::kable(
train_df, booktabs = TRUE,
align = c('r', 'r', 'r'),
col.names = c('나이 (age)', '키 (height)', '몸무게 (weight)'),
caption = '나이, 키, 몸무게 데이터'
)| 나이 (age) | 키 (height) | 몸무게 (weight) |
|---|---|---|
| 21 | 170 | 60 |
| 47 | 167 | 65 |
| 36 | 173 | 67 |
| 15 | 165 | 54 |
| 54 | 168 | 73 |
| 25 | 177 | 71 |
| 32 | 169 | 68 |
| 18 | 172 | 62 |
| 43 | 171 | 66 |
| 28 | 175 | 68 |
회귀모형을 아래와 같이 학습한다.
lm_fit <- lm(weight ~ age + height, data = train_df)추정된 회귀계수는 아래와 같다.
coef(lm_fit)## (Intercept) age height
## -108.1671993 0.3291212 0.9552913추정계수벡터의 분산-공분산 행렬은 아래와 같다.
vcov(lm_fit)## (Intercept) age height
## (Intercept) 1774.3280624 -0.671107283 -10.264885141
## age -0.6711073 0.004794717 0.003035476
## height -10.2648851 0.003035476 0.059566804나이가 40, 키가 170인 사람들의 평균 몸무게에 대한 95% 신뢰구간은 아래와 같이 구할 수 있다.
predict(lm_fit, newdata = tibble(age = 40, height = 170),
interval = "confidence", level = 0.95)## fit lwr upr
## 1 67.39718 65.01701 69.777352.3.1.2 평균 반응치의 분산 추정
새로운 독립변수에 대한 벡터를 아래와 같이 \(\mathbf{x}_0\)라 하면, 평균반응치의 추정량은 아래와 같이 표현된다.
\[\begin{equation} \hat{y}_0 = \mathbf{x}_0^\top \hat{\boldsymbol{\beta}} \tag{2.3} \end{equation}\]
식 (2.3)의 분산은 아래와 같다.
\[\begin{eqnarray} Var(\hat{y}_0) &=& \mathbf{x}_0^\top Var(\hat{\boldsymbol{\beta}}) \mathbf{x}_0\\ &=& \sigma^2 \mathbf{x}_0^\top \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{x}_0 \tag{2.4} \end{eqnarray}\]
위 식 (2.4)에서 \(\sigma^2\) 대신 그 추정값인 \(MSE\) (mean squared error)를 대입하여 평균반응치의 분산을 추정한다.
\[\begin{equation} \hat{Var}(\hat{y}_0) = MSE \times \left( \mathbf{x}_0^\top \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{x}_0 \right) \tag{2.5} \end{equation}\]
우선 Table 2.1에 대해 회귀모형 추정치 \(\hat{\boldsymbol{\beta}}\)와 \(MSE\)값을 구해보자.
n <- nrow(train_df)
X <- cbind(
intercept = rep(1, n),
train_df[, c("age", "height")] %>% as.matrix()
)
y <- train_df[, c("weight")] %>% as.matrix()
k <- ncol(X) - 1
# regression coefficient
beta_hat <- solve(t(X) %*% X) %*% t(X) %*% y
# response estimate
y_hat <- X %*% beta_hat
# MSE
MSE <- sum((y - y_hat) ^ 2) / (n - k - 1)이후, 나이가 40, 키가 170인 객체 \(\mathbf{x}_0\)에 대한 평균 반응치 \(\hat{y}_0\)의 95% 신뢰구간을 구해보자.
# variance of y_hat on new_x
new_x <- matrix(c(
intercept = 1,
age = 40,
height = 170
), ncol = 1)
new_y_hat <- t(new_x) %*% beta_hat
var_new_y_hat <- MSE * t(new_x) %*% solve(t(X) %*% X) %*% new_x
se_new_y_hat <- sqrt(var_new_y_hat)
lci <- new_y_hat + qt(0.025, n - k - 1) * se_new_y_hat
uci <- new_y_hat + qt(0.975, n - k - 1) * se_new_y_hat
str_glue("({format(lci, nsmall = 3L)}, {format(uci, nsmall = 3L)})")## (65.01701, 69.77735)2.3.2 미래반응치의 예측
2.3.2.1 기본 R 스트립트
2.3.1 절에서 추정한 회귀모형을 통해, 새로운 독립변수값(나이 = 40, 키 = 170)을 지닌 특정 객체에 대한 몸무게의 예측구간을 구한다. 이는 한 객체의 몸무게의 예측구간으로, 2.3.1 절에서 구한 평균 몸무게의 신뢰구간보다 넓다.
predict(lm_fit, newdata = tibble(age = 40, height = 170),
interval = "prediction", level = 0.95)## fit lwr upr
## 1 67.39718 60.68745 74.10692.3.2.2 미래 반응치의 예측구간 추정
독립변수값들에 대응하는 미래반응치인 \(y_0\)의 예측치는 평균반응치의 추정치와 동일하며, 반응치의 예측구간을 구하기 위해서는 예측오차의 분산을 알아야 하는데, 이는 아래와 같이 식 (2.4)보다 \(\sigma^2\)이 더 크게 된다.
\[\begin{eqnarray} Var(y_0 - \hat{y}_0) &=& Var(y_0) + Var(\hat{y}_0)\\ &=& \sigma^2 + \sigma^2 \mathbf{x}_0^\top \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{x}_0 \\ &=& \sigma^2 \left( 1 + \mathbf{x}_0^\top \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{x}_0 \right) \tag{2.6} \end{eqnarray}\]
위 식 (2.6)에서 \(\sigma^2\) 대신 \(MSE\)를 대입함으로써 예측오차 분산을 추정할 수 있다.
\[\begin{equation} \hat{Var}(y_0 - \hat{y}_0) = MSE \times \left( 1 + \mathbf{x}_0^\top \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{x}_0 \right) \tag{2.7} \end{equation}\]
앞 절에서 추정한 회귀모형을 이용하여, 나이가 40, 키가 170인 객체 \(\mathbf{x}_0\)에 대한 미래 반응치 \(y_0\)의 95% 예측구간을 구해보자.
# variance of y_hat on new_x
new_x <- matrix(c(
intercept = 1,
age = 40,
height = 170
), ncol = 1)
new_y_hat <- t(new_x) %*% beta_hat
var_new_y_pred <- MSE * (1 + t(new_x) %*% solve(t(X) %*% X) %*% new_x)
se_new_y_pred <- sqrt(var_new_y_pred)
lci <- new_y_hat + qt(0.025, n - k - 1) * se_new_y_pred
uci <- new_y_hat + qt(0.975, n - k - 1) * se_new_y_pred
str_glue("({format(lci, nsmall = 3L)}, {format(uci, nsmall = 3L)})")## (60.68745, 74.1069)2.4 지시변수와 회귀모형
2.4.1 기본 R 스트립트
어떤 열연코일의 인장강도(TS)에 권취온도(CT)가 어떤 영향을 미치는가를 조사하기 위해 TS를 종속변수, CT를 독립변수로 하여 회귀분석을 실시하기로 하였다. 수집된 데이터에는 두 개의 두께 그룹(2mm, 6mm)이 포함되어 있다.
train_df <- tribble(
~ct, ~thickness, ~ts,
540, 2, 52.5,
660, 2, 50.2,
610, 2, 51.3,
710, 2, 49.1,
570, 6, 50.8,
700, 6, 48.7,
560, 6, 51.2,
600, 6, 50.8,
680, 6, 49.3,
530, 6, 51.5
) %>%
mutate(thickness = factor(thickness, levels = c(6, 2)))str(train_df)## tibble [10 × 3] (S3: tbl_df/tbl/data.frame)
## $ ct : num [1:10] 540 660 610 710 570 700 560 600 680 530
## $ thickness: Factor w/ 2 levels "6","2": 2 2 2 2 1 1 1 1 1 1
## $ ts : num [1:10] 52.5 50.2 51.3 49.1 50.8 48.7 51.2 50.8 49.3 51.5두께를 factor로 지정하고 회귀모형을 추정하자.
lm_fit <- lm(ts ~ ct + thickness, data = train_df)회귀 계수는 아래와 같이 얻어진다.
coef(lm_fit)## (Intercept) ct thickness2
## 61.10796610 -0.01767797 0.80415254두께 그룹에 따라 CT에 대한 TS의 기울기가 다르다고 예상되면 CT와 두께 간에 교호작용(interaction)이 존재한다고 말하며, 이 때 회귀모형은 다음과 같이 추정한다.
lm_interaction_fit <- lm(
ts ~ ct + thickness + ct:thickness,
data = train_df
)교호작용이 추가된 회귀 결과는 아래와 같다.
broom::tidy(lm_interaction_fit)## # A tibble: 4 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 60.1 0.750 80.2 2.53e-10
## 2 ct -0.0161 0.00123 -13.1 1.23e- 5
## 3 thickness2 3.28 1.21 2.71 3.52e- 2
## 4 ct:thickness2 -0.00399 0.00194 -2.05 8.57e- 2두께에 따른 CT와 TS의 관계를 그래프로 살펴보자.
new_df <- crossing(
ct = seq(500, 750, by = 10),
thickness = factor(c(6, 2), levels = c(6, 2))
)
new_df %>%
mutate(ts_hat = predict(lm_interaction_fit, .)) %>%
ggplot(aes(x = ct, y = ts_hat)) +
geom_line(aes(color = thickness)) +
geom_point(aes(x = ct, y = ts, color = thickness), data = train_df) +
labs(color = "thickness", x = "CT", y = "TS")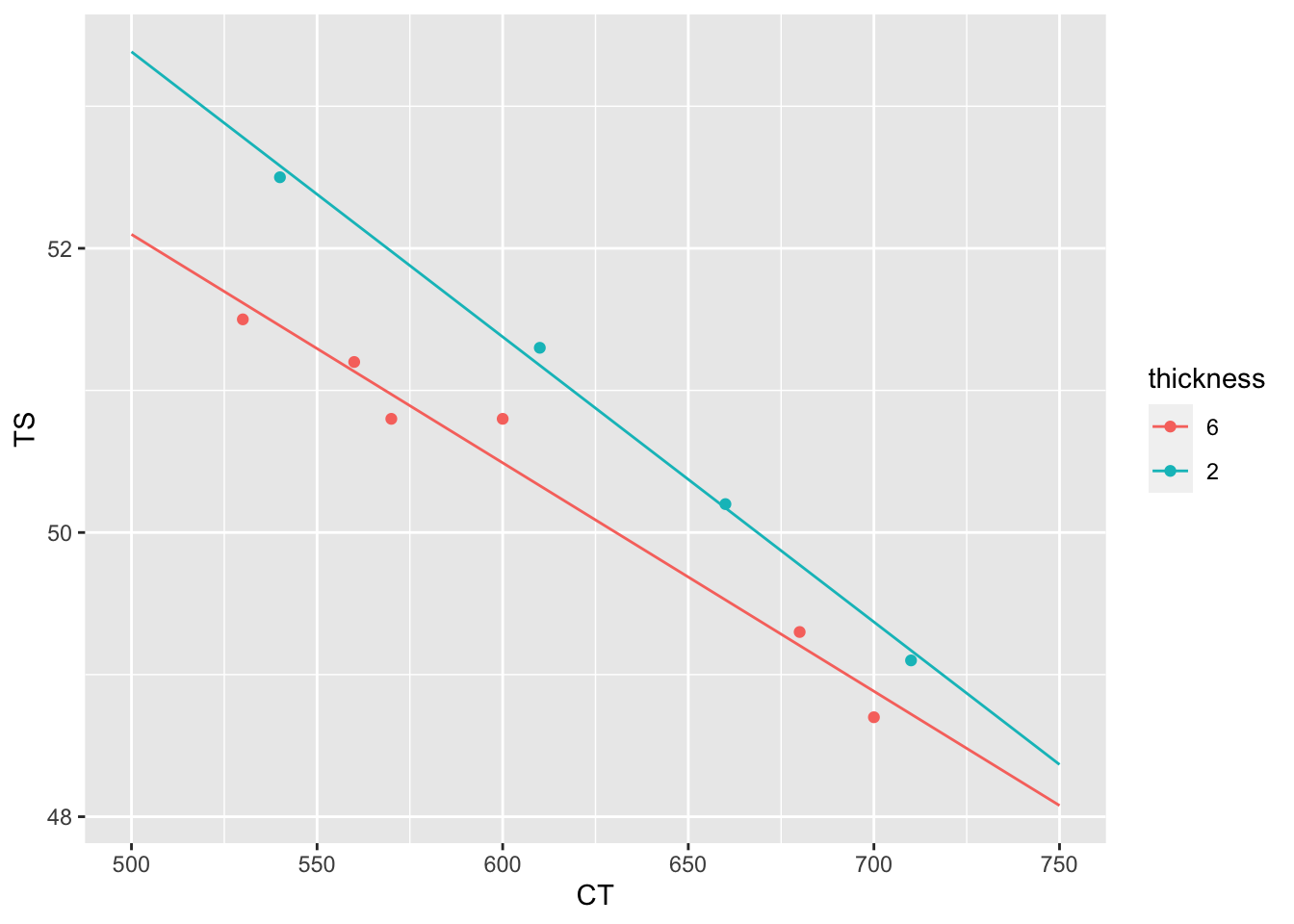
Figure 2.1: 두께에 따른 CT와 TS의 관계